Xét ΔMEN và ΔMEP có

ME chung

EN=EP

MN=MP

Do đó: ΔMEN=ΔMEP

B(-1) = a + 1. (-1)³ + 2. (-1)⁴ - 5a. (-1)² - 6. (-1) + 3a 

         = a + 0 + 3 - 5a + 6 + 3a

         = 9 - a 

BD, CE ở đâu vậy bạn?

\(Q\left(1\right)=a^3+2\cdot1^4-5\cdot1^2-2\cdot1^3-6\cdot1+3\\ =a^3+2\cdot1-5\cdot1-2\cdot1-6\cdot1+3\\ =a^3+2-5-2-6+3\\ =a^3-8\)

\(Q\left(1\right)=a^3+2\cdot1^4-5\cdot1^2-2\cdot1^3-6\cdot1+3\)

\(=a^3+2-5-2-6+3\)

\(=a^3-8\)

Ta có :

\(x^3-3x^2+2x-6\\ =\left(x^3-3x^2\right)+\left(2x-6\right)\\ =x^2\left(x-3\right)+2\left(x-3\right)\\ =\left(x-3\right)\left(x^2+2\right)\)

Vậy `(x-3)(x^2 +2) : (x-3)=x^2+2`

\(\dfrac{x^3-3x^2+2x-6}{x-3}\)

\(=\dfrac{x^2\left(x-3\right)+2\left(x-3\right)}{x-3}\)

\(=x^2+2\)

Bài 1

a) Ta có:

BC > AC > AB (7 > 6 > 4)

⇒ ∠A > ∠B > ∠C (quan hệ giữa góc và cạnh đối diện trong tam giác)

b) Ta có:

∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠B = 180⁰ - (∠A + ∠C)

= 180⁰ - (50⁰ + 50⁰)

= 80⁰

Do ∠A = ∠C = 50⁰

⇒ BC = AB (quan hệ giữa cạnh và góc đối diện)

Do ∠B > ∠A (80⁰ > 50⁰)

⇒ AC > BC

⇒ AC > BC = AB

Bài 2

a) Ta có:

∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)

⇒ ∠C = 180⁰ - (∠A + ∠B)

= 180⁰ - (100⁰ + 40⁰)

= 40⁰

⇒ ∠A là góc lớn nhất

⇒ BC là cạnh lớn nhất (cạnh đối diện với góc lớn nhất)

b) ∆ABC có:

∠B = ∠C = 40⁰

⇒ ∆ABC cân tại A

Ta có:

abcdef = 1000abc + def

Do (abc + def) ⋮ 37

Mà 37 là số nguyên tố

⇒ abc ⋮ 37 và def ⋮ 37

*) abc ⋮ 37

⇒ 1000abc ⋮ 37

⇒ (1000abc + def) ⋮ 37

⇒ abcdef ⋮ 37

a: Xét ΔMAE và ΔMDB có

MA=MD

\(\widehat{AME}=\widehat{DMB}\)(hai góc đối đỉnh)

ME=MB

Do đó: ΔMAE=ΔMDB

=>AE=BD

b: Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}\)

mà AB,AC lần lượt là cạnh đối diện của các góc ACB,ABC

nên AB<AC

Xét ΔABC có AB<AC

mà BD,CD lần lượt là hình chiếu của AB,AC trên BC

nên BD<CD

c: Xét ΔMAF và ΔMDC có

MA=MD

\(\widehat{AMF}=\widehat{DMC}\)(hai góc đối đỉnh)

MF=MC

Do đó: ΔMAF=ΔMDC

=>\(\widehat{MAF}=\widehat{MDC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AF//DC

=>AF//BC

Ta có: ΔMAE=ΔMDB

=>\(\widehat{MAE}=\widehat{MDB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AE//BD

=>AE//BC

Ta có: AE//BC

AF//BC

AE,AF có điểm chung là A

Do đó: E,A,F thẳng hàng

Bổ sung đề; MB\(\perp\)OB tại B

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có

OM chung

\(\widehat{AOM}=\widehat{BOM}\)(OM là phân giác của góc AOB)

Do đó: ΔOAM=ΔOBM

=>MA=MB

b: Ta có: ΔOAM=ΔOBM

=>OA=OB

=>ΔOAB cân tại O

c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có

MA=MB

\(\widehat{AMD}=\widehat{BME}\)(hai góc đối đỉnh)

Do đó: ΔMAD=ΔMBE

=>MD=ME

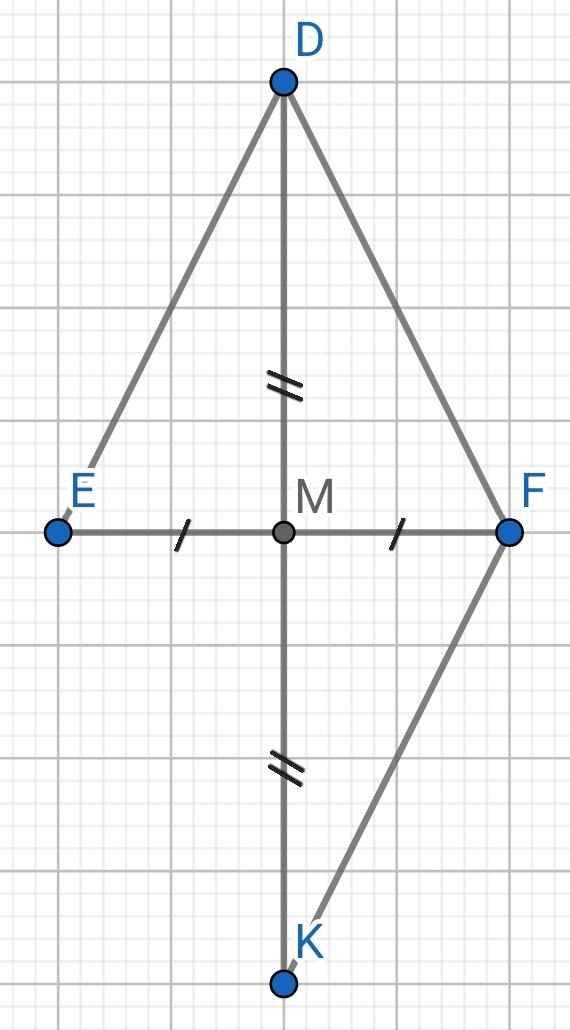
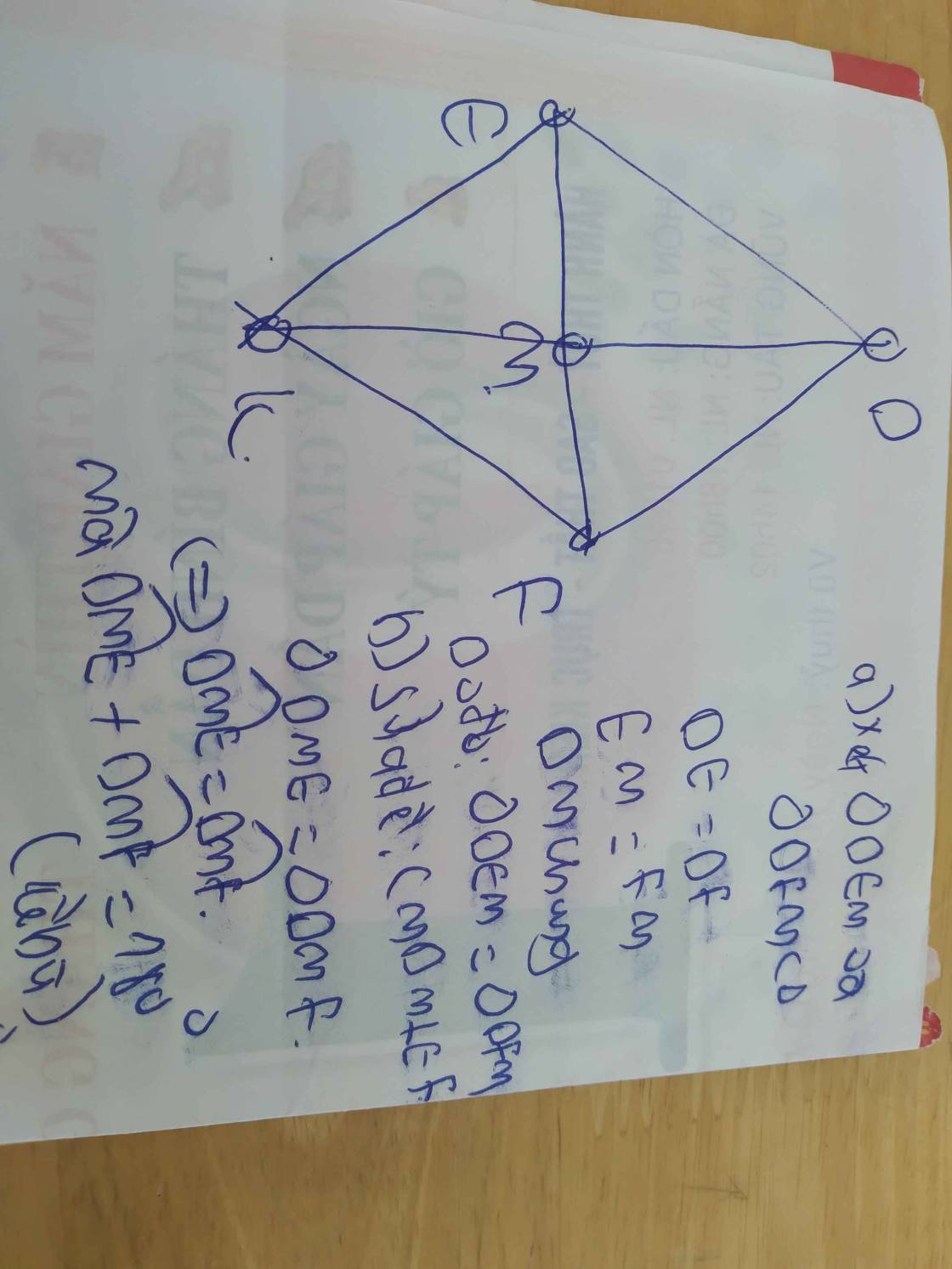
a) Do ∆DEF cân tại D (gt)

⇒ DE = DF

Do M là trung điểm của EF (gt)

⇒ ME = MF

Xét ∆DEM và ∆DFM có:

DE = DF (cmt)

DM là cạnh chung)

ME = MF (cmt)

⇒ ∆DEM = ∆DFM (c-c-c)

b) Sửa đề: Chứng minh DM ⊥ EF

Do ∆DEM = ∆DFM (cmt)

⇒ ∠DME = ∠DMF (hai góc tương ứng)

Mà ∠DME + ∠DMF = 180⁰ (kề bù)

⇒ ∠DME = ∠DMF = 180⁰ : 2 = 90⁰

⇒ DM ⊥ EF

c) Xét ∆DEM và ∆KFM có:

DM = KM (gt)

∠DME = ∠KMF (đối đỉnh)

ME = MF (cmt)

⇒ ∆DEM = ∆KFM (c-g-c)

⇒ DE = KF (hai cạnh tương ứng)

Mà DE = DF (cmt)

⇒ KF = DF

⇒ ∆FDK cân tại F