Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi \(435dm^3=435l\)
Thể tích nước trong bể là:
\(435\text{}\times75\%=326,25\) (l nước)
Đáp số: 326,25 l nước

Khăn thương nhớ ai,
Khăn rơi xuống đất.
Khăn thương nhớ ai,
Khăn vắt lên vai.
Khăn thương nhớ ai,
Khăn chùi nước mắt.
Đèn thương nhớ ai,
Mà đèn không tắt.
Mắt thương nhớ ai,
Mắt ngủ không yên.
Đêm qua em những lo phiền,
Lo vì một nỗi không yên một bề…
Sự vât được nhân hóa ở đây là "Khăn". Nhân hóa bằng cách khiến cho nó biết thương nhớ và có cảm xúc như con người.

8)
a) Tam giác ABI và ACK có:
\(\widehat{AIB}=\widehat{AKC}=90^o;\widehat{BAC}\) chung
\(\Rightarrow\Delta ABI\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AI}{AK}\)
\(\Rightarrow\dfrac{AK}{AC}=\dfrac{AI}{AB}\)
Tam giác AIK và ABC có:
\(\dfrac{AK}{AC}=\dfrac{AI}{AB};\widehat{BAC}\) chung
\(\Rightarrow\Delta AIK\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{S_{AIK}}{S_{ABC}}=\left(\dfrac{AI}{AB}\right)^2=cos^2A\)
\(\Rightarrow S_{AIK}=S_{ABC}.cos^2A\)
b) Có \(S_{BCIK}=S_{ABC}-S_{AIK}\)
\(=S_{ABC}-S_{ABC}.cos^2A\)
\(=S_{ABC}\left(1-cos^2A\right)\)
\(=S_{ABC}.sin^2A\)
c) \(S_{HIK}=S_{ABC}-S_{AKI}-S_{BHK}-S_{CHI}\)
\(=S_{ABC}-S_{ABC}.cos^2A-S_{ABC}.cos^2B-S_{ABC}.cos^2C\)
\(=S_{ABC}\left(1-cos^2A-cos^2B-cos^2C\right)\)
d) Có \(cotB=\dfrac{BH}{AH};cotC=\dfrac{CH}{AH}\)
\(\Rightarrow cotB+cotC=\dfrac{BH}{AH}+\dfrac{CH}{AH}=\dfrac{BC}{AH}\)
Nếu \(cotB+cotC\ge\dfrac{2}{3}\) thì \(\dfrac{BC}{AH}\ge\dfrac{2}{3}\Leftrightarrow BC\ge\dfrac{2}{3}AH\)
Nhưng điều này chưa chắc đã đúng tùy vào cách vẽ hình nên bạn cần bổ sung thêm điều kiện gì đó vào câu này nhé.

Kẻ đường cao BD của tam giác ABC \(\left(D\in AC\right)\)
Khi đó \(AD=AB.cosA=c.cosA\)
\(\Rightarrow CD=AC-AD=b-c.cosA\)
Mặt khác, \(BD=BA.sinA=c\sqrt{1-cos^2A}\)
Tam giác BCD vuông tại D nên:
\(a^2=BC^2=DB^2+DC^2\)
\(=\left(b-c.cosA\right)^2+\left(c\sqrt{1-cos^2A}\right)^2\)
\(=b^2-2bc.cosA+c^2.cos^2A+c^2\left(1-cos^2A\right)\)
\(=b^2+c^2-2bc.cosA\)
Vậy đẳng thức được chứng minh.


Đây là toán nâng cao chuyên đề lập số theo điều kiện cho trước, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải
Từ 205 đến 2025 các số chia hết cho 9 là các số thuộc dãy số sau:
207; 216; 225; ...; 2025
Dãy số trên là dãy số cách đều với khoảng cách là: 216 -207 = 9
Số số hạng của dãy số trên là: (2025 - 207) : 9 + 1 = 203 (số)
Từ 205 đến 2025 có số số hạng là:
(2025 - 205) : 1 + 1 = 1821 (số)
Từ 205 đến 2025 số các số không chia hết cho 9 là:
1821 - 203 = 1618 (số)
Đáp số:...


Lời giải:
PT $\Leftrightarrow (x-1)\left(\frac{1}{13}+\frac{1}{14}-\frac{1}{15}-\frac{1}{16}\right)=0$
Hiển nhiên $\frac{1}{13}+\frac{1}{14}>\frac{1}{15}+\frac{1}{16}$
$\Rightarrow \frac{1}{13}+\frac{1}{14}-\frac{1}{15}-\frac{1}{16}>0$
$\Rightarrow x-1=0$
$\Rightarrow x=1$
Vậy PT có nghiệm duy nhất $x=1$.
P/s: Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

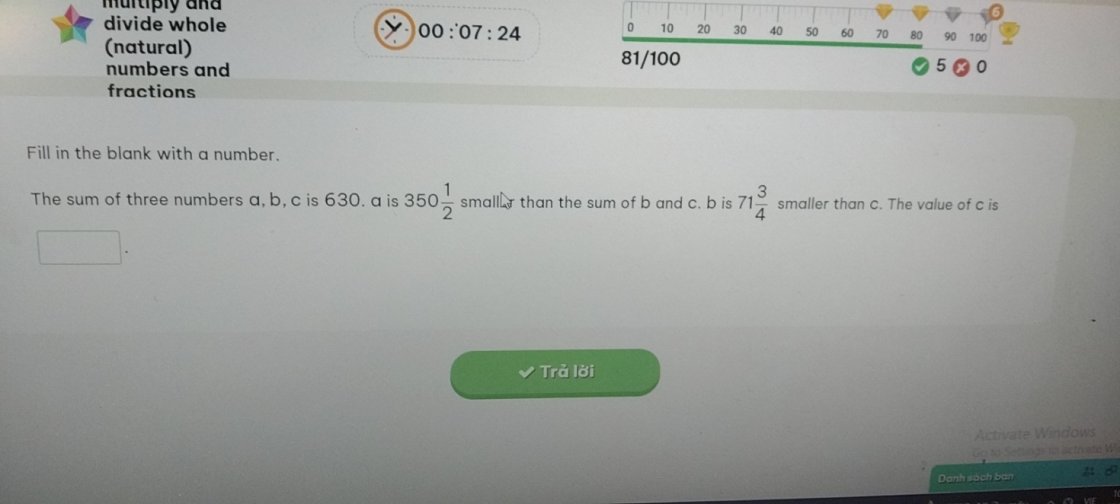
nhờ thầy cô dịch giúp bài này ak.
Tổng của ba số a; b; c là 630
a nhỏ hơn tổng của hai số b và c là 350\(\dfrac{1}{2}\)
b nhỏ hơn c là 71\(\dfrac{3}{4}\)
Tìm giá trị của c