1. Giải phương trình: 9x + 3.6x = 4x+1
2. Cho phương trình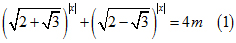 với m là tham số.
với m là tham số.
a) Giải phương trình (1) với m = 1
b) Tìm m để phương trình (1) có nghiệm duy nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(D=ℝ\)
Có \(y'=x^2-2x-m\)
Xét \(y'=0\)
\(\Leftrightarrow x^2-2x-m=0\)
\(\Leftrightarrow m=x^2-2x\) (1)
YCBT \(\Leftrightarrow\) (1) có 2 nghiệm phân biệt thuộc \(\left(3;4\right)\)
Đặt \(f\left(x\right)=x^2-2x\). Khi đó \(f'\left(x\right)=2x-2\)
\(f'\left(x\right)=0\Leftrightarrow x=1\)
Lập BBT, ta thấy để \(m=f\left(x\right)\) có 2 nghiệm phân biệt thuộc \(\left(3;4\right)\) thì \(3< m< 8\)
Khi đó \(m\in\left\{4;5;6;7\right\}\), suy ra có 4 giá trị nguyên của m thỏa mãn ycbt.
-> Chọn B.

Chọn `D.` Thế năng cực đại tại vị trí vận tốc đổi chiều.
- Vì:
Khi vận tốc của vật đổi chiều thì lúc đó vật đang ở vị trí biên dương (hoặc biên âm) `=>x=+-A`.
Mà `W_t =1/2 kx^2`
`=>W_t=1/2 kA^2 =W_[t(max)]`

#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,A[100],i,kt,j;
cin>>n;
for (int i=1; i<=n; i++)
cin>>A[i];
for (int i=1; i<=n; i++)
if (A[i]>1)
{
kt=0;
for (int j=2; j*j<=A[i]; j++)
if (A[i]%j==0) kt=1;
if (kt==0) cout<<A[i]<<" ";
}
return 0;
}

b) Xét pt hoành độ giao điểm của hàm số đã cho và Ox là \(2x^3+2\left(6m-1\right)x^2-3\left(2m-1\right)x-3\left(1+2m\right)=0\) (*)
Ta thấy \(x=1\) là nghiệm của pt trên. Lập sơ đồ Horner:
| \(2\) | \(2\left(6m-1\right)\) | \(-3\left(2m-1\right)\) | \(-3\left(1+2m\right)\) | |
| \(x=1\) | \(2\) | \(12m\) | \(6m+3\) | \(0\) |
Do đó pt (*)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+12mx+6m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x^2+12mx+6m+3=0\end{matrix}\right.\)
Xét pt \(2x^2+12mx+6m+3=0\) (1)
Ycbt \(\Leftrightarrow\) pt (1) có 2 nghiệm phân biệt \(x_1,x_2\) khác 1 và thỏa mãn \(x_1^2+x_2^2=27\)
Có \(\Delta'=\left(6m\right)^2-2\left(6m+3\right)=36m^2-12m-6>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{1+\sqrt{7}}{6}\\m< \dfrac{1-\sqrt{7}}{6}\end{matrix}\right.\)
Có 2 nghiệm khác 1 \(\Leftrightarrow2.1^2+12m.1+6m+3\ne0\)
\(\Leftrightarrow18m+5\ne0\)
\(\Leftrightarrow m\ne-\dfrac{5}{18}\)
Theo định lý Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-6m\\x_1x_2=\dfrac{6m+3}{2}\end{matrix}\right.\)
Để \(x_1^2+x_2^2=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=27\)
\(\Leftrightarrow\left(-6m\right)^2-2.\dfrac{6m+3}{2}=27\)
\(\Leftrightarrow36m^2-6m-3=27\)
\(\Leftrightarrow6m^2-m-5=0\)
\(\Leftrightarrow6m^2-6m+5m-5=0\)
\(\Leftrightarrow6m\left(m-1\right)+5\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(6m+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(nhận\right)\\m=-\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy \(m=1\) hoặc \(m=-\dfrac{5}{6}\) thỏa ycbt.
c) Xét pt \(x^3-3mx^2+\left(3m-1\right)x+6m=0\) (*)
Ta thấy (*) có nghiệm \(x=-1\). Lập sơ đồ Horner:
| \(1\) | \(-3m\) | \(3m-1\) | \(6m\) | |
| \(x=-1\) | \(1\) | \(-3m-1\) | \(6m\) | \(0\) |
Vậy (*) \(\Leftrightarrow\left(x+1\right)\left(x^2-\left(3m+1\right)x+6m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2-\left(3m+1\right)x+6m=0\end{matrix}\right.\)
Tới đây thì làm tương tự câu b) nhé.
1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)