Bắn liên tiếp 3 viên đạn vào một mục tiêu. Xác suất trúng đích của mỗi viên đạn là 0,59. Gọi X là số viên đạn không trúng đích trong 3 viên đạn. Lập bảng phân bố xác suất của X và tính EX, DX.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1: \(u_4=u_1+3k\)
=>\(3k=\dfrac{3}{8}-3=\dfrac{3}{8}-\dfrac{24}{8}=-\dfrac{21}{8}\)
=>\(k=-\dfrac{7}{8}\)
\(u_7=u_1+6k=3+6\cdot\dfrac{-7}{8}=3-\dfrac{42}{8}=\dfrac{24-42}{8}=-\dfrac{18}{8}=-\dfrac{9}{4}\)
Câu 2:
\(\dfrac{u_5}{u_8}=8\)
=>\(\dfrac{u_1\cdot q^4}{u_1\cdot q^7}=8\)
=>\(\dfrac{1}{q^3}=8\)
=>\(q=\dfrac{1}{2}\)
\(u_{12}=u_1\cdot q^{11}=12\cdot\left(\dfrac{1}{2}\right)^{11}=\dfrac{12}{2^{11}}=\dfrac{3}{2^9}\)
Câu 3:
Tổng của 5 số hạng đầu là:
\(S_5=\dfrac{u_1\cdot\left(1-q^5\right)}{1-q}=\dfrac{2\cdot\left(1-4^5\right)}{1-4}=682\)
=>Chọn D

Câu 25:
\(0< \alpha< \dfrac{\Omega}{2}\)
=>\(0< sin\alpha< 1;0< cos\alpha< 1\)
\(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}\)
\(=\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\)
\(=\dfrac{1+sin\alpha+1-sin\alpha}{cos\alpha}=\dfrac{2}{cos\alpha}\)
Câu 28:
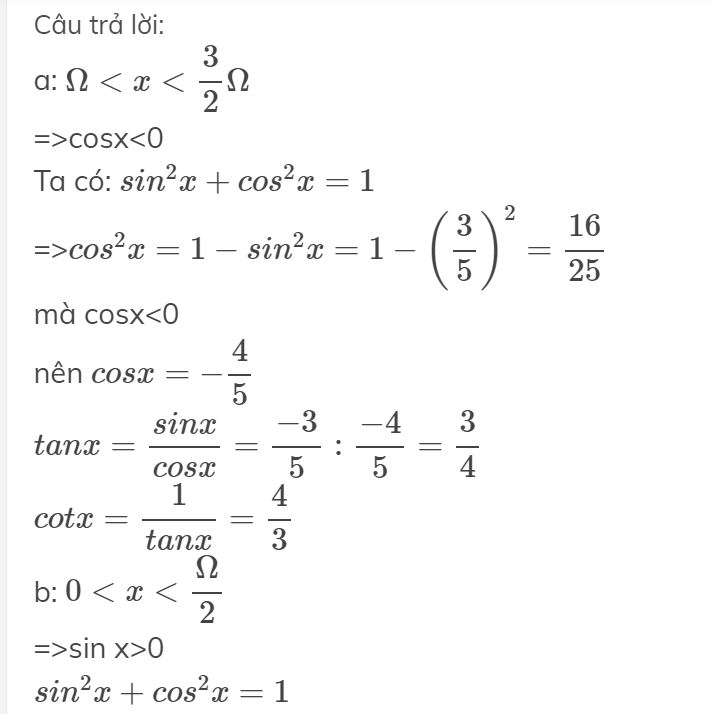
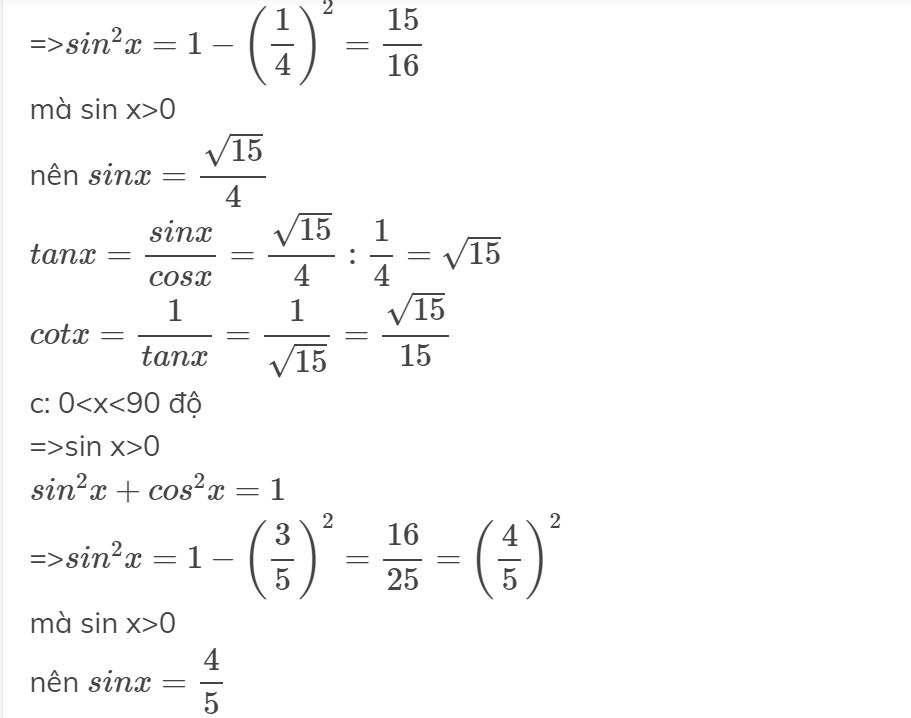


a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)

\(A=2\cdot cos\left(\dfrac{\Omega}{2}+x\right)+sin\left(5\Omega-x\right)+sin\left(\dfrac{3\Omega}{2}+x\right)+cos\left(\dfrac{\Omega}{2}+x\right)\)
\(=3\cdot cos\left(\dfrac{\Omega}{2}+x\right)+sin\left(\Omega-x\right)+sin\left(\dfrac{\Omega}{2}+\Omega+x\right)\)
\(=-3\cdot sinx+sinx+cos\left(\Omega+x\right)\)
\(=-2\cdot sinx-cosx\)
\(B=sin\left(\Omega+x\right)-cos\left(\dfrac{\Omega}{2}+x\right)+cot\left(2\Omega-x\right)+tan\left(\dfrac{2\Omega}{2}+x\right)\)
\(=-sinx+sinx+cot\left(-x\right)+tan\left(x\right)\)
\(=tanx-cotx=tanx-\dfrac{1}{tanx}=\dfrac{tan^2x-1}{tanx}\)

1. After finishing her studying, Trang went out with her friends.
2. Before eating lunch, the kids washed their hands.
3. We arrived at the cinema when the film had already started at 7 p.m.
4. After preparing the meal, my aunt picked up her son.
5. Before my mother came home, my sister had watered all the plants in the garden.
6. Tracy got bad marks because she hadn't revised the lessons carefully.
7. Before we started working, the manager had explained everything clearly.
8. My sister applied for a job in a big city after she had graduated from university.
9. After ironing all the clothes, I took out the trash.
10. He tasted that kind of food for the first time.

Câu 1:
\(2\sin x-\sqrt{3}=0\\ \Leftrightarrow\sin x=\dfrac{\sqrt{3}}{2}=\sin\dfrac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{\pi}{3}+k_12\pi\\x_2=\pi-\dfrac{\pi}{3}+k_22\pi=\dfrac{2\pi}{3}+k_22\pi\end{matrix}\right.\left(k_1,k_2\inℤ\right)\)
Mà: \(x\in\left[0;2\pi\right]\) do đó nên: \(k_1=0,k_2=0\)
Vậy tập nghiệm pt là: \(S=\left\{\dfrac{\pi}{3};\dfrac{2\pi}{3}\right\}\) (2 nghiệm => D)
Câu 2:
Vì: \(-1\le\cos x\le1\forall x\)
\(\Rightarrow-1\le m+1\le1\\ \Leftrightarrow-2\le m\le0\)
Mà: \(m\inℤ\Rightarrow m\in\left\{-2;-1;0\right\}\) (C)
Câu 1: \(2\cdot sinx-\sqrt{3}=0\)
=>\(sinx=\dfrac{\sqrt{3}}{2}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+k2\Omega\\x=\Omega-\dfrac{\Omega}{3}+k2\Omega=\dfrac{2}{3}\Omega+k2\Omega\end{matrix}\right.\)
Để \(x\in\left[0;2\Omega\right]\) thì \(\left[{}\begin{matrix}\dfrac{\Omega}{3}+k2\Omega\in\left[0;2\Omega\right]\\\dfrac{2}{3}\Omega+k2\Omega\in\left[0;2\Omega\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2k+\dfrac{1}{3}\in\left[0;2\right]\\2k+\dfrac{2}{3}\in\left[0;2\right]\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}2k\in\left[-\dfrac{1}{3};\dfrac{5}{3}\right]\\2k\in\left[-\dfrac{2}{3};\dfrac{4}{3}\right]\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}k\in\left[-\dfrac{1}{6};\dfrac{5}{6}\right]\\k\in\left[-\dfrac{1}{3};\dfrac{2}{3}\right]\end{matrix}\right.\Leftrightarrow k=0\)
=>Chọn B
Câu 2:
Để phương trình cosx =m+1 có nghiệm thì -1<=m+1<=1
=>-2<=m<=0
mà m nguyên
nên \(m\in\left\{-2;-1;0\right\}\)
=>Chọn C

a: \(cos\left(x-15^0\right)=\dfrac{\sqrt{2}}{2}\)
=>\(\left[{}\begin{matrix}x-15^0=45^0+k\cdot360^0\\x-15^0=-45^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=60^0+k\cdot360^0\\x=-30^0+k\cdot360^0\end{matrix}\right.\)
b: \(cos\left(2x+\dfrac{\Omega}{3}\right)+cos\left(x-\dfrac{\Omega}{3}\right)=0\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=-cos\left(x-\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(\Omega-x+\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(-x+\dfrac{4\Omega}{3}\right)\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{3}=-x+\dfrac{4\Omega}{3}+k2\Omega\\2x+\dfrac{\Omega}{3}=x-\dfrac{4}{3}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\Omega+k2\Omega\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+\dfrac{k2\Omega}{3}\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
c: \(sin\left(3x+1\right)=sin\left(x-2\right)\)
=>\(\left[{}\begin{matrix}3x+1=x-2+k2\Omega\\3x+1=\Omega-x+2+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-3+k2\Omega\\4x=1+\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}+k\Omega\\x=\dfrac{1}{4}+\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\end{matrix}\right.\)
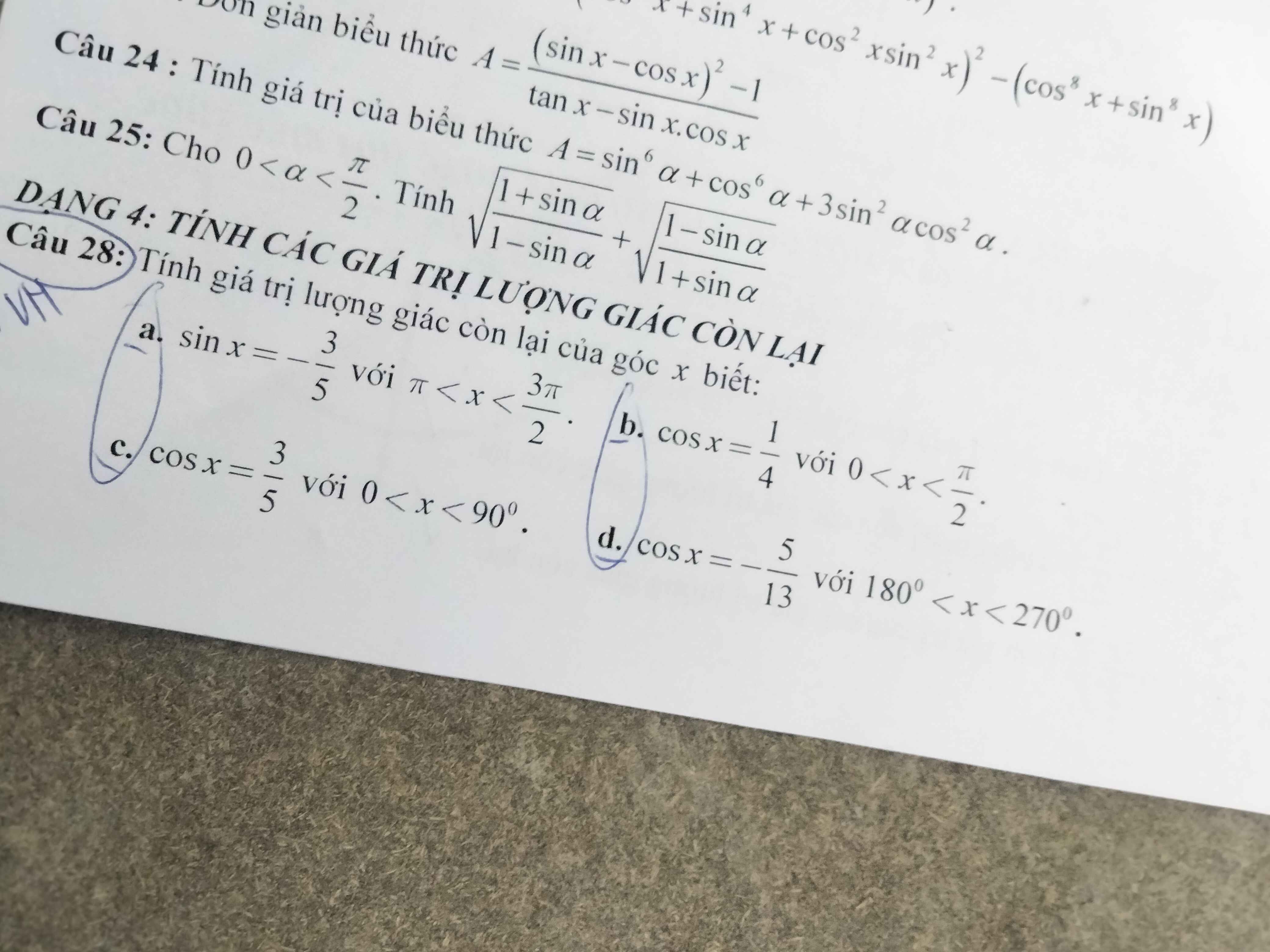
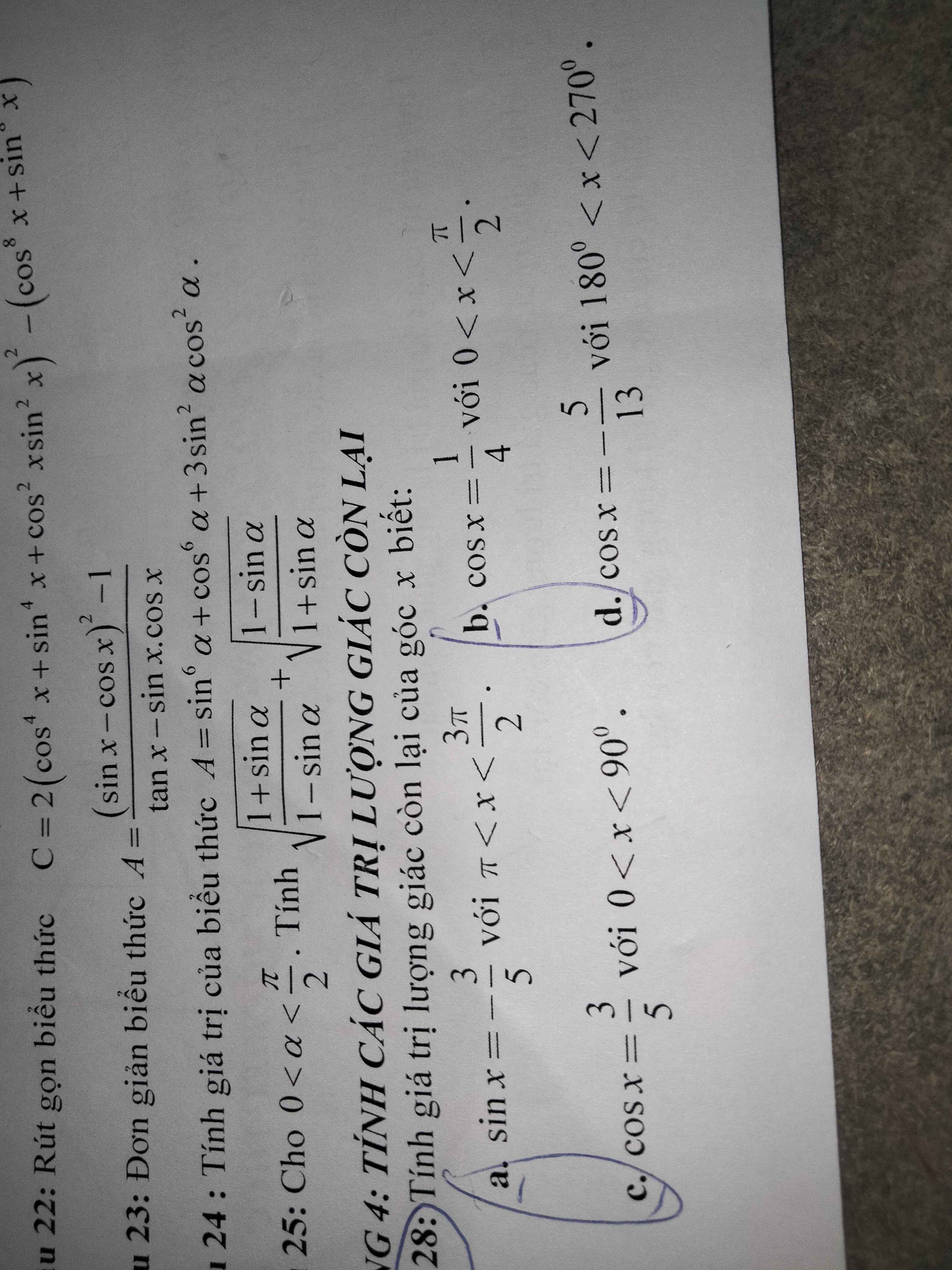

 Tick mình nha bạn!
Tick mình nha bạn!