Tìm giá trị lớn nhất của biểu thức A= -x2 -6x+1
Mọi người giúp mình với ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x-1)(x+2)-x(x-2)-3x
=x2+x-2-x2+2x-3x
=-2 <=>Bt =-2 mọi x
Vậy bt =-2 khi x=-100

a) Độ dài trung đoạn của hình chóp S.ABC là độ dài đoạn thẳng từ trung điểm của cạnh đáy đến đỉnh của hình chóp. Vì tam giác ABC là tam giác đều, nên ta có thể tính độ dài trung đoạn bằng cách sử dụng công thức Pythagoras: Trung đoạn = căn bậc hai của (AC^2 - (AC/2)^2) = căn bậc hai của (8^2 - (8/2)^2) = căn bậc hai của (64 - 16) = căn bậc hai của 48 = 4 căn 3 cm
b) Diện tích xung quanh của hình chóp S.ABC là tổng diện tích các mặt bên của hình chóp. Vì tam giác ABC là tam giác đều, nên diện tích mặt bên của hình chóp là diện tích tam giác đều. Ta có công thức tính diện tích tam giác đều: Diện tích tam giác đều = (cạnh^2 * căn 3) / 4 = (8^2 * căn 3) / 4 = 16 căn 3 cm^2
Diện tích xung quanh = Diện tích tam giác đều + Diện tích đáy = 16 căn 3 + 27,72 = 16 căn 3 + 27,72 cm^2
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh và diện tích đáy: Diện tích toàn phần = Diện tích xung quanh + Diện tích đáy = 16 căn 3 + 27,72 + 27,72 = 16 căn 3 + 55,44 cm^2
c) Thể tích của hình chóp tam giác đều S.ABC được tính bằng công thức: Thể tích = (Diện tích đáy * Chiều cao) / 3 = (27,72 * 7,5) / 3 = 69,3 cm^3

Ta sẽ chứng minh cần ít nhất 21 người. Thật vậy, nếu có ít nhất 21 người tham gia đường đua thì do có tổng cộng 10 con đường khác nhau nên theo nguyên lí Diriclet tồn tại 1 con đường có từ 3 người tham gia trở lên.
Với trường hợp có 20 người tham gia, ta chỉ ra 1 trường hợp không thỏa mãn:
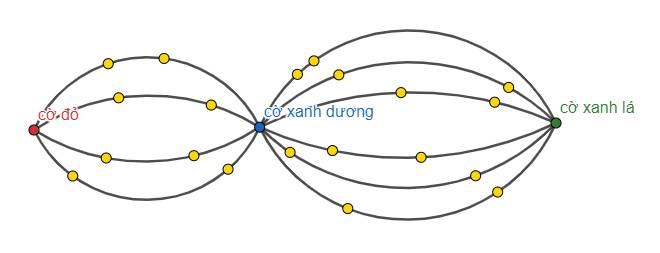
Ta dễ dàng lập những sơ đồ tương tự để chứng minh nếu có \(\le19\) người tham gia thì không đảm bảo điều kiện đề bài.
Như vậy cần có ít nhất 21 người tham gia để đảm bảo điều kiện bài toán được thỏa mãn.

(n - 1)(3 - 2n) - n(n + 5)
= 3n - 2n² - 3 + 2n - n² - 5n
= (-2n² - n²) + (3n + 2n - 5n) - 3
= -3n² - 3
= -3(n² + 1) 3 với mọi n ∈ R
Vậy biểu thức đã cho chia hết cho 3 với mọi n ∈ R

\(\left(x-y\right)^2=x^2-2xy+y^2=\)
\(=\left(x^2+2xy+y^2\right)-4xy=\)
\(=\left(x+y\right)^2-4xy=15^2-4.40=65\)
A = -x² - 6x + 1
= -(x² + 6x - 1)
= -(x² + 6x + 9 - 10)
= -[(x + 3)² - 10]
= -(x + 3)² + 10
Do (x + 3)² ≥ 0 với mọi x ∈ R
⇒ -(x + 3)² ≤ 0 với mọi x ∈ R
⇒ -(x + 3)² + 10 ≤ 10 với mọi x ∈ R
Vậy GTLN của A là 10 khi x = -3
\(A=-x^2-6x+1\)
\(A=-\left(x^2+6x-1\right)\)
\(A=-\left(x^2+6x+9-10\right)\)
\(A=-\left(x^2+2\cdot x\cdot3+3^2\right)+10\)
\(A=-\left(x+3\right)^2+10\)
Có: \(\left(x+3\right)^2\ge0\forall x\Rightarrow-\left(x+3\right)^2\le0\)
\(\Rightarrow-\left(x+3\right)^2+10\le10\)
\(\Rightarrow A\le10\)
Dấu "=" xảy ra khi \(\left(x+3\right)^2=0\Leftrightarrow x+3=0\)
\(\Leftrightarrow x=-3\)
Vậy: \(A_{min}=10\Leftrightarrow x=-3\)