ngu

Thay vì viết vào đây bạn có thể cop ra mạng để cha mà=)?

6235515

6235515

760 > 750 > 700 > 650

Vậy nồi cơm tiêu thụ ít năng lượng hơn là nồi thứ ba

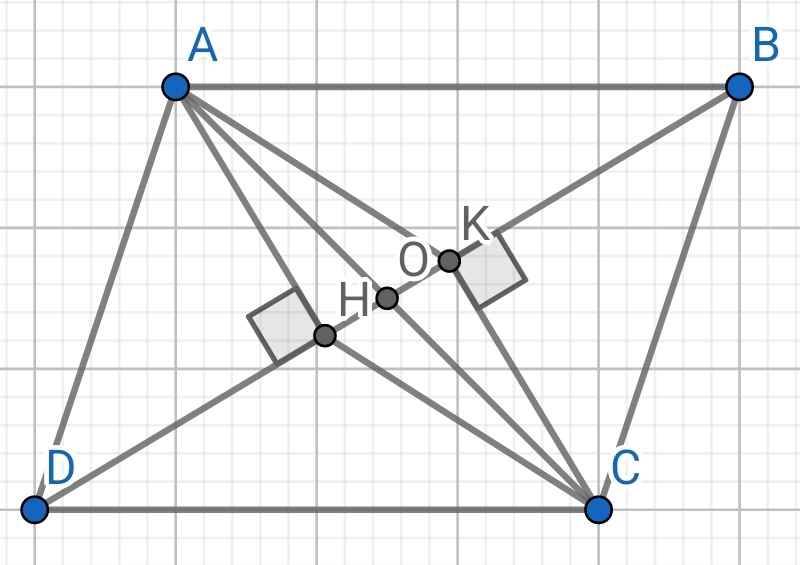
a) Do ABCD là hình bình hành (gt)

⇒ AD // BC

⇒ ∠ADB = ∠CBD (so le trong)

⇒ ∠ADH = ∠CBK

Do ABCD là hình bình hành (gt)

⇒ AD = BC

Xét hai tam giác vuông: ∆ADH và ∆CBK có:

AD = BC (cmt)

∠ADH = ∠CBK (cmt)

⇒ ∆ADH = ∆CBK (cạnh huyền - góc nhọn)

⇒ AH = CK (hai cạnh tương ứng)

Do AH ⊥ BD (gt)

CK ⊥ BD (gt)

⇒ AH // CK

Tứ giác AHCK có:

AH // CK (cmt)

AH = CK (cmt)

⇒ AHCK là hình bình hành

b) Do AHCK là hình bình hành (cmt)

O là trung điểm của HK (gt)

⇒ O là trung điểm của AC

⇒ A, O, C thẳng hàng

\(x\cdot\left(x^2-3\right)-x^3+7=0\\ x^3-3x-x^3+7=0\\ -3x+7=0\\ -3x=-7\\ x=\dfrac{7}{3}\)

Tôi chịu

a) Do ABCD là hình bình hành (gt)

⇒ AD // BC

⇒ ∠ADB = ∠CBD (so le trong)

⇒ ∠ADH = ∠CBK

Do ABCD là hình bình hành (gt)

⇒ AD = BC

Xét hai tam giác vuông: ∆ADH và ∆CBK có:

AD = BC (cmt)

∠ADH = ∠CBK (cmt)

⇒ ∆ADH = ∆CBK (cạnh huyền - góc nhọn)

⇒ AH = CK (hai cạnh tương ứng)

Do AH ⊥ BD (gt)

CK ⊥ BD (gt)

⇒ AH // CK

Tứ giác AHCK có:

AH // CK (cmt)

AH = CK (cmt)

⇒ AHCK là hình bình hành

b) Do AHCK là hình bình hành (cmt)

O là trung điểm của HK (gt)

⇒ O là trung điểm của AC

⇒ A, O, C thẳng hàng

21/23 × 5/15 × 23

= (21/23 × 23) × 5/15

= 21 × 1/3

= 7

ko biết

Chiều dài mảnh giấy:

25/4 × 2 = 25/2 (cm)

Chu vi mảnh giấy:

(25/4 + 25/2) × 2 = 75/2 (cm)

Diện tích mảnh giấy:

25/2 × 25/4 = 625/8 (cm²)

            Giải:

Chiều dài của mảnh giấy màu hình chữ nhật là: \(\dfrac{25}{4}\) x 2 = \(\dfrac{25}{2}\) (cm)

Chu vi của hình chữ nhật là: (\(\dfrac{25}{2}\) + \(\dfrac{25}{4}\)) x 2 = \(\dfrac{75}{2}\) (cm)

Diện tích của hình chữ nhật là: \(\dfrac{25}{2}\) x \(\dfrac{25}{4}\) = \(\dfrac{625}{8}\) (cm²)

Đáp số:...