\(2a=3b;5b=7c\)

\(\Rightarrow\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\)

\(\Rightarrow\dfrac{a}{21}=\dfrac{b}{14};\dfrac{b}{14}=\dfrac{c}{10}\)

\(\Rightarrow\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}\)

\(\Rightarrow\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}\)

Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}=\dfrac{3a-7b+5c}{63-98+50}=-\dfrac{30}{15}=-2\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{21}=-2\Leftrightarrow a=-42\\\dfrac{b}{14}=-2\Leftrightarrow b=-28\\\dfrac{c}{10}=-2\Leftrightarrow c=20\end{matrix}\right.\)

AP = AC - PC = AC - \(\dfrac{2}{3}\)AC = \(\dfrac{1}{3}\)AC

S_ABP = \(\dfrac{1}{3}\)S_ABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy Ac và AP = \(\dfrac{1}{3}\) AC)

S_APM  = \(\dfrac{1}{3}\)S_ABP (vì hai tam giác có chung chiều cao hạ từ đỉnh  P xuống đáy AB và AM = \(\dfrac{1}{3}\) AB)

S_APM = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{1}{3}\)S_ABC = \(\dfrac{1}{9}\)S_ABC

Tương tự ta có:

S_CPN = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{2}{3}\)S_ABC = \(\dfrac{2}{9}\)S_ABC

S_BMN = \(\dfrac{2}{3}\)\(\times\)\(\dfrac{2}{3}\)S_ABC = \(\dfrac{4}{9}\)S_ABC

S_PMN = S_ABC - (\(\dfrac{1}{9}\)S_ABC + \(\dfrac{2}{9}\)S_ABC + \(\dfrac{4}{9}\)S_ABC)

S_PMN = S_ABC  - \(\dfrac{7}{9}\)S_ABC = \(\dfrac{2}{9}\)S_ABC

S_PMN = 135 x \(\dfrac{2}{9}\) = 30 (cm²)

Đs..

...!

   Chiều cao của thửa ruộng hình thang là: 30 x 2 : 15  = 4 (m)

    Ta có sơ đồ:

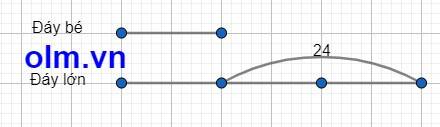
Teo sơ đồ ta có:

Đáy bé của thửa ruộng hình thang là: 24 : ( 3 - 1) = 12 (m)

Đáy lớn của thửa ruộng hình thang là: 12 + 24  = 36 (m)

Diện tích thửa ruộng hình thang là: (36 + 12) x 4 : 2 =  96 (m²)

Đs.. 

Bài 1:

a; \(\dfrac{5}{18}\) + \(\dfrac{8}{19}\) - \(\dfrac{7}{21}\) + (- \(\dfrac{10}{36}\) + \(\dfrac{11}{19}\)  + \(\dfrac{1}{3}\)) - \(\dfrac{5}{8}\)

=  \(\dfrac{5}{18}\) + \(\dfrac{8}{19}\) - \(\dfrac{1}{3}\) -\(\dfrac{10}{36}\) + \(\dfrac{11}{19}\) + \(\dfrac{1}{3}\) - \(\dfrac{5}{8}\)

= (\(\dfrac{5}{18}\) - \(\dfrac{10}{36}\)) + (\(\dfrac{8}{19}\) + \(\dfrac{11}{19}\)) - (\(\dfrac{1}{3}\) - \(\dfrac{1}{3}\)) - \(\dfrac{5}{8}\)

= (\(\dfrac{5}{18}\) - \(\dfrac{5}{18}\)) + \(\dfrac{19}{19}\) - 0 - \(\dfrac{5}{8}\)

= 0 + 1 - \(\dfrac{5}{8}\)

= \(\dfrac{3}{8}\)

b; \(\dfrac{1}{13}\) + (\(\dfrac{-5}{18}\) - \(\dfrac{1}{13}\) + \(\dfrac{12}{17}\)) - (\(\dfrac{12}{17}\) - \(\dfrac{5}{18}\) + \(\dfrac{7}{5}\))

= \(\dfrac{1}{13}\) - \(\dfrac{5}{18}\) - \(\dfrac{1}{13}\) + \(\dfrac{12}{17}\) - \(\dfrac{12}{17}\) + \(\dfrac{5}{18}\) - \(\dfrac{7}{5}\)

= (\(\dfrac{1}{13}\) - \(\dfrac{1}{13}\)) + (\(\dfrac{12}{17}\) - \(\dfrac{12}{17}\)) + (-\(\dfrac{5}{18}\) + \(\dfrac{5}{18}\)) - \(\dfrac{7}{5}\)

= 0 + 0 + 0 - \(\dfrac{7}{5}\)

= - \(\dfrac{7}{5}\)

Bài 1 c;

   \(\dfrac{15}{14}\) - (\(\dfrac{17}{23}\) - \(\dfrac{80}{87}\) + \(\dfrac{5}{4}\)) + (\(\dfrac{17}{23}\) - \(\dfrac{15}{14}\) + \(\dfrac{1}{4}\))

=  \(\dfrac{15}{14}\) - \(\dfrac{17}{23}\) + \(\dfrac{80}{87}\) - \(\dfrac{5}{4}\) + \(\dfrac{17}{23}\) - \(\dfrac{15}{14}\) + \(\dfrac{1}{4}\)

= (\(\dfrac{15}{14}-\dfrac{15}{14}\)) + (\(-\dfrac{17}{23}+\dfrac{17}{23}\)) - (\(\dfrac{5}{4}\) - \(\dfrac{1}{4}\)) + \(\dfrac{80}{87}\)

= 0 + 0 - 1 + \(\dfrac{80}{87}\)

= - \(\dfrac{7}{87}\)

Đổi \(1\dfrac{1}{2}=\dfrac{1\times2+1}{2}=\dfrac{3}{2}=1,5\)

Chu vi hình tròn đó là:

\(1,5\times2\times3,14=9,42\)

Đáp số: \(9,42\)

Đổi \(1\dfrac{1}{2}=\dfrac{3}{2}=1,5\)

Chu vi hình tròn đó là:

\(1,5\times2\times3,14=9,42\)

                        Đáp số:\(9,42\)

Tick cho mik nhé

Là sao vậy bạn,không có diện tích hình thang và diện tích hình tam giác làm sao mà tính được.

đúng luôn ko có diện tích ABCD và BCE

660 16 41 4

=47

chịu

giúp tôi với

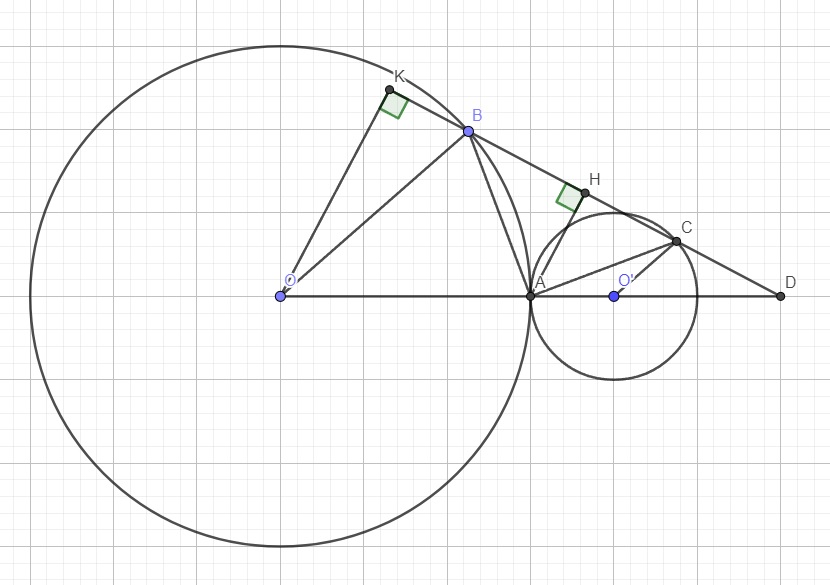
a.

OB song song O'C \(\Rightarrow\widehat{BOA}+\widehat{CO'A}=180^0\) (hai góc trong cùng phía)

Do \(OA=OB=R\) và \(O'A=O'C=R'\) nên các tam giác OAB và O'AC cân tại O và O'

\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\widehat{OBA}\\\widehat{O'AC}=\widehat{O'CA}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\dfrac{180^0-\widehat{BOA}}{2}\\\widehat{O'AC}=\dfrac{180^0-\widehat{CO'A}}{2}\end{matrix}\right.\) 

\(\Rightarrow\widehat{BAC}=180^0-\left(\widehat{OAB}+\widehat{O'AC}\right)=180^0-\left(\dfrac{180^0-\widehat{BOA}}{2}+\dfrac{180^0-\widehat{CO'A}}{2}\right)\)

\(=180^0-\left(180^0-\dfrac{\widehat{BOA}+\widehat{CO'A}}{2}\right)=90^0\)

\(\Rightarrow\Delta ABC\) vuông tại A

b.

TH1:

Nếu \(R=R'\) thì OBCO' là hình bình hành (cặp cạnh đối OB, O'C song song và bằng nhau)

\(\Rightarrow BC||O'O\Rightarrow AH\perp O'O\)

Từ B kẻ \(BK\perp O'O\Rightarrow AHBK\) là hình chữ nhật (tức giác có 3 góc vuông)

\(\Rightarrow AH=BK\le OB=R=R'\)

Dấu "=" xảy ra khi K trùng O hay BC vuông góc OB \(\Rightarrow BC\) là tiếp tuyến của (O)

TH2:

Nếu \(R\ne R'\), không mất tính tổng quát giả sử \(R>R'\)

Kéo dài BC và O'O cắt nhau tại D

Từ O kẻ \(OK\perp BC\)

Áp dụng định lý Talet: \(\dfrac{DO'}{DO}=\dfrac{OC'}{OB}=\dfrac{R'}{R}\)

OK và AH cùng vuông góc BC \(\Rightarrow OK||AH\)

Áp dụng định lý Thales:

\(\dfrac{AH}{OK}=\dfrac{DO'}{DO}=\dfrac{R'}{R}\Rightarrow AH=\dfrac{R'}{R}.OK\)

\(\Rightarrow AH_{max}\) khi \(OK_{max}\)

Mà \(OK\perp BC\Rightarrow OK\le OB\) (đường vuông góc ko lớn hơn đường xiên)

\(\Rightarrow OK_{max}=OB=R\)

\(\Rightarrow AH_{max}=\dfrac{R'}{R}.R=R'\)

Dấu "=" xảy ra khi K trùng B hay BC là tiếp tuyến của (O)