 giúp mik với ạ -)
giúp mik với ạ -)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Diện tích sắt cần để làm lồng sắt là:
\(2\times\left(4+1\right)\times2+2\times4\times1=28\left(m^2\right)\)
Làm lồng sắt hết số tiền là:
\(28\times39000=1092000\left(đ\right)\)
ĐS: ...

\(a)4^7:2^5\\ =\left(2^2\right)^7:2^5\\ =2^{14}:2^5\\ =2^9\\ b)3^{10}:9^3\\ =3^{10}:\left(3^2\right)^3\\ =3^{10}:3^6\\ =3^4\\ c)27^9:3^{10}\\ \left(3^3\right)^9:3^{10}\\ =3^{27}:3^{10}\\ =3^{17}\\ d)25^5:5^3\\ =\left(5^2\right)^5:5^3\\ =5^{10}:5^3\\ =5^7\\ e)36^7:6^4\\ =\left(6^2\right)^7:6^4\\ =6^{14}:6^4\\ =6^{10}\\ g)4^3\cdot8^4\\ =\left(2^2\right)^3\cdot\left(2^3\right)^4\\ =2^6\cdot3^{12}\\ =2^{18}\)

Olm chào em,hiện tại yêu cầu của em chưa cụ thể, vậy em vui lòng đăng lại câu hỏi để được sự trợ giúp tốt nhất từ olm cho tài khoản vip em nhé.

\(\left(\dfrac{2}{3}\right)^8:\left(\dfrac{4}{9}\right)^3\\ =\left[\left(\dfrac{2}{3}\right)^2\right]^4:\left(\dfrac{4}{9}\right)^3\\ =\left(\dfrac{4}{9}\right)^4:\left(\dfrac{4}{9}\right)^3\\ =\dfrac{4}{9}\)
\(27^3:3^2\\ =\left(3^3\right)^3:3^2\\ =3^9:3^2\\ =3^7\\ =2187\)
\(\left(-\dfrac{3}{5}\right)^4:\left(\dfrac{5}{2}\right)^4\\ =\left(-\dfrac{3}{5}:\dfrac{5}{2}\right)^4\\ =\left(-\dfrac{6}{25}\right)^4\)
\(\left(\dfrac{3}{5}\right)^{12}:\left(\dfrac{9}{25}\right)^5\\ =\left(\dfrac{3}{5}\right)^{12}:\left[\left(\dfrac{3}{5}\right)^2\right]^5\\ =\left(\dfrac{3}{5}\right)^{12}:\left(\dfrac{3}{5}\right)^{10}\\ =\left(\dfrac{3}{5}\right)^2\\ =\dfrac{9}{25}\)
\(\left(\dfrac{2}{3}\right)^8:\left(\dfrac{4}{9}\right)^3=\left(\dfrac{4}{9}\right)^4:\left(\dfrac{4}{9}\right)^3=\dfrac{4}{9}\)
\(27^3:3^2=3^9:3^2=3^7=2187\)

a) Ta có:
\(64^8=\left(2^6\right)^8=2^{6\cdot8}=2^{48}\)
\(16^{12}=\left(2^4\right)^{12}=2^{4\cdot12}=2^{48}\)
\(\Rightarrow64^8=16^{12}\)
b) Ta có:
\(\left(\dfrac{1}{16}\right)^{10}=\left[\left(\dfrac{1}{2}\right)^4\right]^{10}=\left(\dfrac{1}{2}\right)^{4\cdot10}=\left(\dfrac{1}{2}\right)^{40}\)
Mà: 50 > 40 => `(1/2)^50<(1/2)^40`
c) Ta có:
\(\left(\dfrac{9}{16}\right)^{100}=\left[\left(\dfrac{3}{4}\right)^2\right]^{100}=\left(\dfrac{3}{4}\right)^{200}\)
Mà: `3/4>2/3=>(3/4)^200>(2/3)^200`
\(^{^{ }}\)a,64^8=16^12
b,(1/16)^10<(1/2)^50
c,(2/3)^200>(9/16)^100
CỦA BẠN ĐÂY NẾU SAI THÌ CHO MÌNH XIN LỖI NHÉ

a; 25 x 53 x \(\dfrac{1}{625}\) x 52
= 52 x 53 x \(\dfrac{1}{5^4}\) x 52
= 55 x \(\dfrac{1}{5^4}\) x 52
= 5 x 52
= 53
a)
\(25\cdot5^3\cdot\dfrac{1}{625}\cdot5^2\\ =\left(5^2\cdot5^3\cdot5^2\right)\cdot\dfrac{1}{625}\\ =5^7\cdot\dfrac{1}{5^4}\\ =5^3\)
b)
\(5^2\cdot3^5\cdot\left(\dfrac{3}{5}\right)^2\\ =5^2\cdot3^5\cdot\dfrac{3^2}{5^2}\\ =3^5\cdot3^2\\ =3^7\)
c)
\(\left(-\dfrac{1}{7}\right)^4\cdot49^2\\ =\dfrac{\left(-1\right)^4}{7^4}\cdot\left(7^2\right)^2\\ =\dfrac{1}{7^4}\cdot7^4\\ =1\)
d)
\(\left(\dfrac{1}{16}\right)^2:\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{8}\right)^3\\ =\left[\left(\dfrac{1}{2}\right)^4\right]^2:\left(\dfrac{1}{2}\right)^4\cdot\left[\left(-\dfrac{1}{2}\right)^3\right]^3\\ =\left(\dfrac{1}{2}\right)^8:\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{2}\right)^9\\ =\left(\dfrac{1}{2}\right)^4\cdot\left(-\dfrac{1}{2}\right)^9\\ =\left(\dfrac{1}{2}\right)^4\cdot-\left(\dfrac{1}{2}\right)^9\\ =-\left(\dfrac{1}{2}\right)^{13}\)

a; \(x\) : (- \(\dfrac{1}{3}\))3 = \(\dfrac{1}{9}\)
\(x\) : (\(-\dfrac{1}{27}\)) = \(\dfrac{1}{9}\)
\(x\) = \(\dfrac{1}{9}\) x (- \(\dfrac{1}{27}\))
\(x\) = - \(\dfrac{1}{243}\)
Vậy \(x\) = - \(\dfrac{1}{243}\)
b; (\(\dfrac{4}{5}\))5 x \(x\) = (\(\dfrac{4}{5}\))7
\(x\) = (\(\dfrac{4}{5}\))7 : (\(\dfrac{4}{5}\))5
\(x\) = \(\dfrac{4^7}{5^7}\) : \(\dfrac{4^5}{5^5}\)
\(x\) = \(\dfrac{4^7}{5^7}\) x \(\dfrac{5^5}{4^5}\)
\(x\) = \(\dfrac{4^2}{5^2}\)
\(x\) = \(\dfrac{16}{25}\)
Vậy \(x\) = \(\dfrac{16}{25}\)
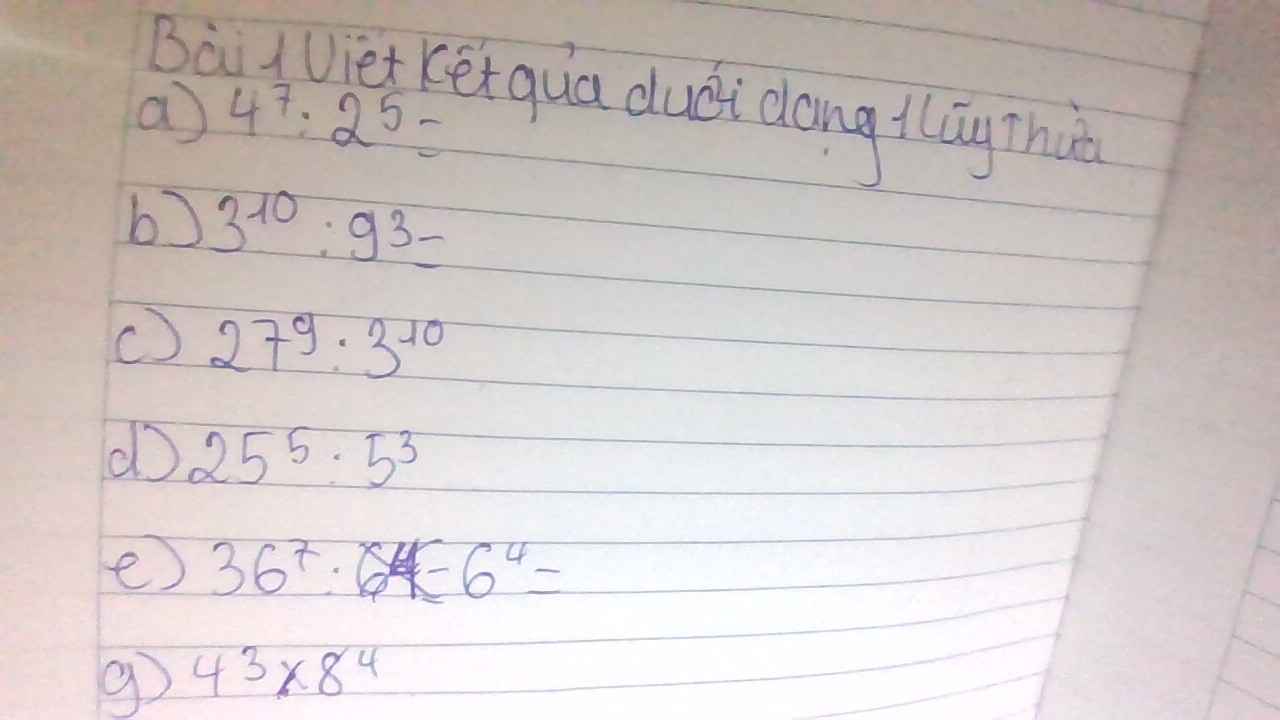
2:
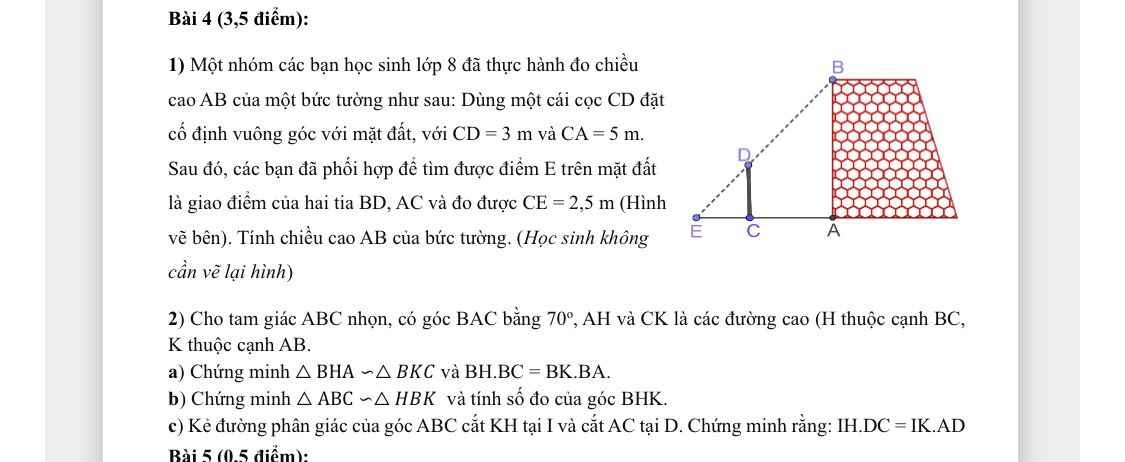
a: Xét ΔBHA vuông tại H và ΔBKC vuông tại K có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBKC
=>\(\dfrac{BH}{BK}=\dfrac{BA}{BC}\)(2)
=>\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
=>\(BH\cdot BC=BK\cdot BA\)
b: Xét ΔBHK và ΔBAC có
\(\dfrac{BH}{BA}=\dfrac{BK}{BC}\)
\(\widehat{HBK}\) chung
Do đó: ΔBHK~ΔBAC
=>\(\widehat{BHK}=\widehat{BAC}=70^0\)
c: Xét ΔBKH có BI là phân giác
nên \(\dfrac{IH}{IK}=\dfrac{BH}{BK}\left(1\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{IH}{IK}=\dfrac{DA}{DC}\)
=>\(IH\cdot DC=DA\cdot IK\)