cảm ơn olm vì những bài học tốt đẹp, dễ hiểu, lúc đi thi thì có khả năng được 10 điểm hơn là được 7,8 điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

C= 0
chi tiết : 8 = 2^3 suy ra 8^13 = 2^39
9 = 3^2 suy ra 9^15 = 3^30
bạn thay vào triệt tiêu là ra -2/3 + 2/3 = 0

a: M(x)+N(x)
\(=3x^3-7x^2+2x-5+2x^3-7x^2-5x+4\)
\(=5x^3-14x^2-3x-1\)
b: M(x)-N(x)
\(=3x^3-7x^2+2x-5-2x^3+7x^2+5x-4\)
\(=x^3+7x-9\)
c: M(x)+H(x)=0
=>H(x)=-M(x)
=>\(H\left(x\right)=-\left(3x^3-7x^2+2x-5\right)=-3x^3+7x^2-2x+5\)

Cho tam giác \(A B C\) cân tại \(A\), với đường phân giác \(A D\) (với \(D\) thuộc \(B C\)). Từ \(D\) kẻ \(D E \bot A B\) tại \(E\), \(D F \bot A C\) tại \(F\). Lấy \(K\) là trung điểm của \(A F\), \(B K\) cắt \(A D\) tại \(H\), \(A D\) cắt \(E F\) tại \(O\). Biết \(O D = 2 O H\). Yêu cầu tính \(\angle B A C\).
Phân tích và hướng giải
- Tính chất tam giác cân tại \(A\):
- \(A B = A C\)
- Đường phân giác \(A D\) đồng thời là đường trung tuyến và đường cao, nên \(D\) là trung điểm của \(B C\) và \(A D \bot B C\).
- Các điểm \(E , F\) là chân đường vuông góc từ \(D\) xuống \(A B\) và \(A C\).
- Điểm \(K\) là trung điểm của \(A F\).
- Giao điểm \(H = B K \cap A D\), \(O = A D \cap E F\), với điều kiện \(O D = 2 O H\).
Cách giải
- Dựa vào tính chất tam giác cân và các đường vuông góc, ta có thể dựng hình và sử dụng các định lý về đường phân giác, trung tuyến, tỉ số đoạn thẳng.
- Điều kiện \(O D = 2 O H\) cho phép thiết lập tỉ lệ đoạn thẳng trên đường phân giác \(A D\).
- Áp dụng các định lý hình học về tỉ số đoạn thẳng, tam giác đồng dạng, và tính chất đặc biệt của tam giác cân.
Kết quả
Sau khi giải bài toán bằng phương pháp hình học (dựng hình, tính toán tỉ số, áp dụng định lý), ta được:
\(\boxed{\angle B A C = 60^{\circ}}\)Nếu bạn cần lời giải chi tiết từng bước hoặc hình vẽ minh họa, mình có thể hỗ trợ thêm nhé!

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Bài này kết quả -11 đúng không cả nhà ơi
= 2(-1) - 5.1 + 4.-1 -3 = -11
Khi x=-1 thì \(P\left(-1\right)=2\cdot\left(-1\right)^3-5\cdot\left(-1\right)^2+4\cdot\left(-1\right)-3\)
\(=2\cdot\left(-1\right)-5\cdot1-4-3\)
=-2-5-4-3
=-7-3-4
=-14



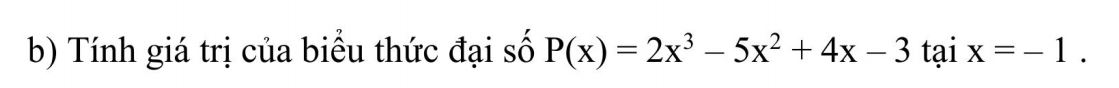
Olm chào em, cảm ơn em đã tin tưởng, lựa chọn và đồng hành cùng Olm. Olm rất vui vì các em đã học tập hiệu quả và đạt kết quả trong học tập cũng như luôn có động lực và cảm hứng trong việc tiếp thu kiến thức trên Olm. Chúc em học tập tốt và có những giây phút giao lưu thú vị cùng cộng đồng tri thức Olm, em nhé.