c++:

#include <iostream>

using namespace std;

int main(){

int y;

cin >> y;

int i = 1;

int luythua = 1;

while(i<=y){

luythua = luythua *i;

i = i+1;

}

cout << luythua;

}

with open("a.txt", "r") as f:

     numbers = list(map(int, f.readline().split()))

product = 1

for number in numbers:

     product *= number

print("Tích các số trong file a.txt là:", product)

Họ Geometridae

bài đấy làm như thế nào ạ

A

a

a. Em kiểm tra lại đề bài xem có nhầm lẫn đâu không.

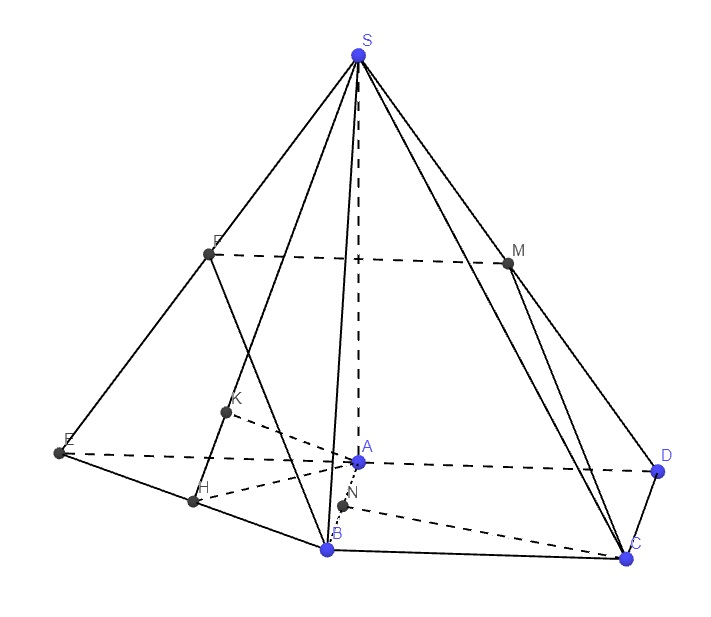
Ta có CN cắt AB tại N (do N là trung điểm AB) nên không tồn tại \(d\left(CN,AB\right)\) (chỉ có khoảng cách giữa 2 đường thẳng song song hoặc chéo nhau chứ không có khoảng cách giữa 2 đường thẳng cắt nhau).

b.

Gọi E là điểm đối xứng D qua A \(\Rightarrow DE=2AD=2BC\), gọi F là trung điểm SE.

\(\Rightarrow MF\) là đường trung bình tam giác SDE \(\Rightarrow\left\{{}\begin{matrix}MF=\dfrac{1}{2}DE=BC\\MF||DE||BC\end{matrix}\right.\)

\(\Rightarrow\) Tứ giác BCMF là hình bình hành \(\Rightarrow CM||BF\)

Lại có AM là đường trung bình tam giác SDE \(\Rightarrow AM||SE\)

\(\Rightarrow\left(ACM\right)||\left(SBE\right)\Rightarrow d\left(SB,CM\right)=d\left(\left(ACM\right),\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)

Gọi H là trung điểm BE, do \(AE=AD=AB\Rightarrow\Delta ABE\) vuông cân tại A

\(\Rightarrow AH\perp BE\Rightarrow BE\perp\left(SAH\right)\)

Trong mp (SAH), từ A kẻ \(AK\perp SH\) \(\Rightarrow AK\perp\left(SBE\right)\)

\(\Rightarrow AK=d\left(A;\left(SBE\right)\right)=d\left(SB,CM\right)\)

\(AH=\dfrac{1}{2}BE=\dfrac{1}{2}\sqrt{AB^2+AE^2}=\dfrac{a\sqrt{2}}{2}\)

Áp dụng hệ thức lượng trong tam giác vuông SAH:

\(AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{a\sqrt{21}}{7}\)

a/ Ta có: AB vuông góc với BC, SC vuông góc với BC (vì SC vuông góc với mặt đáy ABCD). Vậy AB // SC. Vậy AB vuông góc (SBC).

b/ Tương tự, ta có: AD vuông góc với CD, SC vuông góc với CD. Vậy AD // SC. Vậy AD vuông góc (SCD).

c/ Ta có: SA vuông góc với mặt đáy ABCD (vì S là đỉnh chóp), CI vuông góc với SB (vì đường thẳng CI là hình chiếu của đường thẳng SC lên mặt phẳng chứa SB và CI). Vậy SA // CI. Vậy SA vuông góc CI.

d/ Gọi M là trung điểm của IJ. Ta cần chứng minh SA vuông góc CM. Ta có: CM vuông góc với IJ (vì nằm trên đường trung trực của IJ). Ta cũng có: SA vuông góc CI (đã chứng minh ở câu c). Vậy ta cần chứng minh CI // JM. Từ đó suy ra (SAC) ⊥ (CIJ). Theo tính chất của hình học không gian, ta có CI vuông góc với mặt phẳng (SBC). Tương tự, JI vuông góc với mặt phẳng (SCD). Vậy CI // JI. Điều này suy ra từ tính chất của mặt phẳng và đoạn thẳng vuông góc với mặt phẳng. Suốt đoạn thẳng IJ, ta có thể lấy một điểm nào đó làm trung điểm, ví dụ M. Vậy CI // JM.

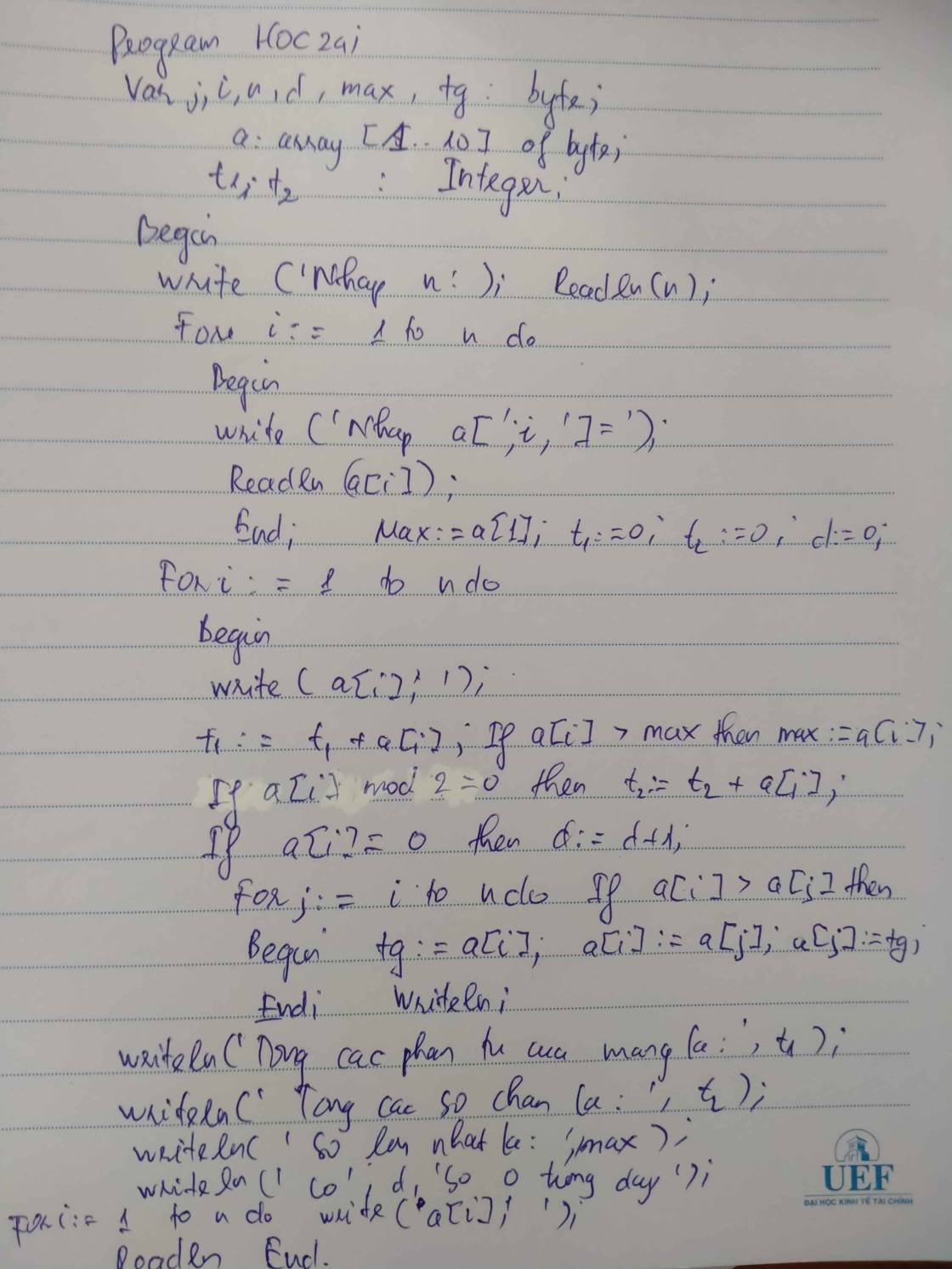
CAU TRA LOI LA EM KO BIET

a, 12

b, 376

c,0.12