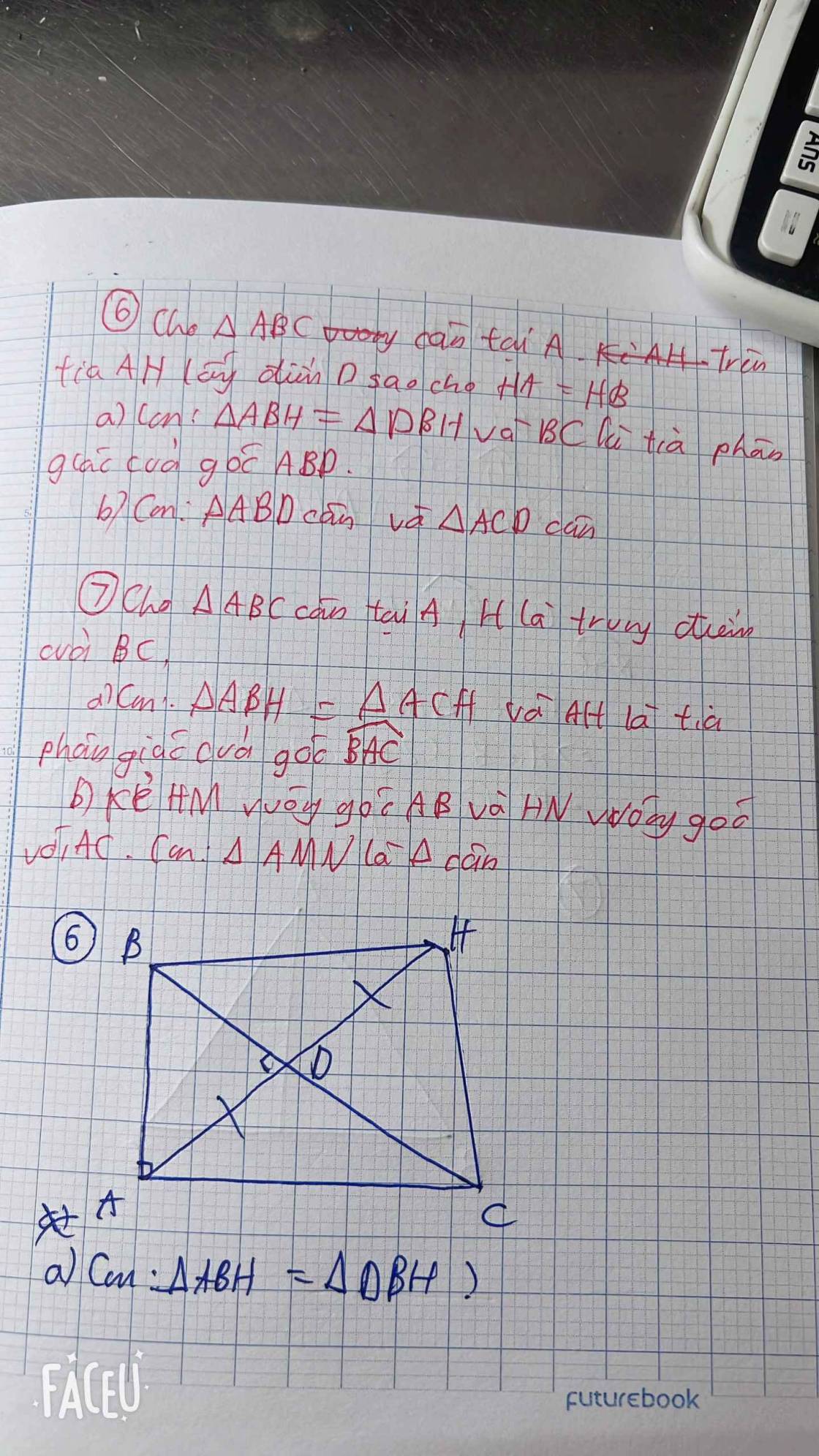
Bài 1: Sửa đề: Chứng minh ΔABM=ΔACM

Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

Bài 2:

a: Xét ΔAMC và ΔDMB có

MA=MD

\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)

MC=MB

Do đó: ΔAMC=ΔDMB

b: Xét ΔBAE có

BH là đường cao

BH là đường trung tuyến

Do đó: ΔBAE cân tại B

=>BA=BE

\(x^2y-y+xy^2-x+2\\=(x^2y+xy^2)-(x+y)+2\\=xy(x+y)-(x+y)+2\\=2\cdot(-2)-(-2)+2\\=0\)

A B C M N O H d

a/

Xét tg vuông AHO và tg vuông BHO có

AH=BH; OH chung => tg AHO = tg BHO (hai tg vuông có 2 cạnh góc vuông bằng nhau)

=> OA=OB (1)

=> tg OAB cân tại O \(\Rightarrow\widehat{OAB}=\widehat{OBA}\) (góc ở đáy tg cân) (2)

Ta có

AM+AN=AB (gt) => AN=AB-AM

BM=AB-AM

=> AN=BM (3)

Từ (1) (2) (3) => tg BOM = tg AON (c.g.c)

b/

Từ O dựng đường thẳng d vuông góc với MN

=> d là đường cao của tg OMN

Ta có

tg BOM = tg AON (cmt) => OM=ON => tg OMN cân tại O

=> d là đường trung trực của tg OMN hay d là đường trung trực của MN (Trong tg cân đường cao xuất phát từ đỉnh tg cân đồng thời là đường trung trực)

Ta có OH là đường trung trực của AB cố định; AO là đường phân giác của \(\widehat{A}\) không đổi => O cố dịnh

=> d luôn đi qua O cố định

Số chẵn là một số nguyên chia hết cho 2

Cảm ơn bạn nha

a: \(f\left(x\right)=2x^3+2x+x^2-2x^3-x+1\)

\(=\left(2x^3-2x^3\right)+x^2+2x-x+1=x^2+x+1\)

b: \(h\left(x\right)-f\left(x\right)=2x^2-x-1\)

=>\(h\left(x\right)=2x^2-x-1+x^2+x+1\)

=>\(h\left(x\right)=3x^2\)

c: \(f\left(x\right)\cdot\left(x-1\right)=\left(x^2+x+1\right)\left(x-1\right)\)

\(=x^3-x^2+x^2-x+x-1=x^3-1\)

Bài 2:

a: \(\dfrac{a}{5}=\dfrac{b}{7}\)

mà a-b=10

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a-b}{5-7}=\dfrac{10}{-2}=-5\)

=>\(a=-5\cdot5=-25;b=-5\cdot7=-35\)

b: \(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}\)

mà a-2b+c=18

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{-4}=\dfrac{b}{6}=\dfrac{c}{7}=\dfrac{a-2b+c}{-4-2\cdot6+7}=\dfrac{18}{-9}=-2\)

=>\(\left\{{}\begin{matrix}a=\left(-2\right)\cdot\left(-4\right)=8\\b=-2\cdot6=-12\\c=-2\cdot7=-14\end{matrix}\right.\)

Bài 3:

Gọi độ dài ba cạnh lần lượt là a(cm),b(cm),c(cm)

(Điều kiện: a>0; b>0; c>0)

Độ dài ba cạnh lần lượt tỉ lệ với 3;7;5 nên \(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}\)

Chu vi tam giác là 105cm nên a+b+c=105

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3}=\dfrac{b}{7}=\dfrac{c}{5}=\dfrac{a+b+c}{3+7+5}=\dfrac{105}{15}=7\)

=>\(a=7\cdot3=21\left(nhận\right);b=7\cdot7=49\left(nhận\right);c=7\cdot5=35\left(nhận\right)\)

Vậy: Độ dài ba cạnh là 21cm; 49cm; 35cm

Bài 6

Em ghi đề sai rồi

Bài 7

a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Do H là trung điểm của BC (gt)

⇒ HB = HC

Xét ∆ABH và ∆ACH có:

AB = AC (cmt)

AH là cạnh chung

HB = HC (cmt)

⇒ ∆ABH = ∆ACH (c-c-c)

⇒ ∠BAH = ∠CAH (hai góc tương ứng)

⇒ AH là tia phân giác của ∠BAC

b) Do ∠BAH = ∠CAH (cmt)

⇒ ∠MAH = ∠NAH

Xét hai tam giác vuông: ∆AHM và ∆AHN có:

AH là cạnh chung

∠MAH = ∠NAH (cmt)

⇒ ∆AHM = ∆AHN (cạnh góc vuông - góc nhọn kề)

⇒ AM = AN (hai cạnh tương ứng)

⇒ ∆AMN cân tại A

205: \(f\left(x\right)=x^2-x+1\)

\(=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}>0\forall x\)

=>f(x) không có nghiệm thực

204:

a: \(f\left(-1\right)=\left(-1\right)^4+5\cdot\left(-1\right)^3+3\cdot\left(-1\right)^2+2\cdot\left(-1\right)+3\)

\(=1-5+3-2+3\)

=7-7=0

=>x=-1 là nghiệm của f(x)

\(g\left(-1\right)=3\cdot\left(-1\right)^4+\left(-1\right)^3+\left(-1\right)^2-7\cdot\left(-1\right)-10\)

\(=3-1+1+7-10=10-10=0\)

=>x=-1 là nghiệm của g(x)

\(h\left(-1\right)=4\cdot\left(-1\right)^3+2\cdot\left(-1\right)^2-\left(-1\right)+1\)

\(=-4+2+1+1=0\)

=>x=-1 là nghiệm của h(x)

khoảng 40-45

40-45 kg

Cho:

Điền hệ số thích hợp vào ô trống.
�(�)+�(�)=P(x)+Q(x)= ((�3x3)) ++ ((�2x2))++ ((�x)) ++ (())

P(x)+Q(x)

\(=3x^2-3x+6+4x^3-5x^2+x-3\)

\(=4x^3-2x^2-2x+3\)