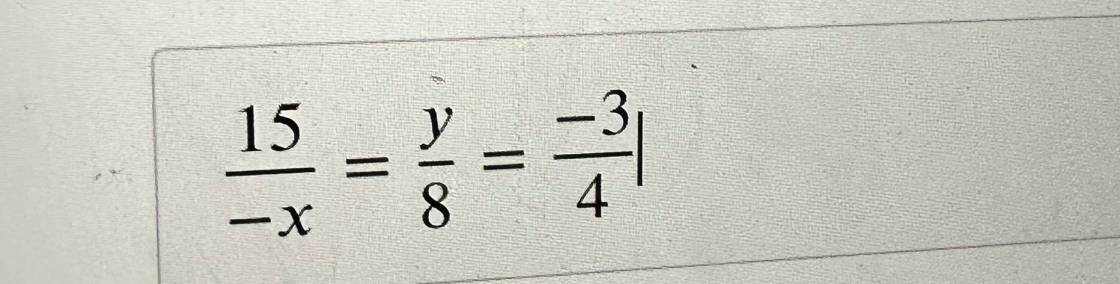15/(-x) = -3/4

-x.(-3) = 15.4

3x = 60

x = 60 : 3

x = 20

y/8 = -3/4

4y = 8.(-3)

4y = -24

y = -24 : 4

y = -6

Câu 1

∆' = [-(m + 1)]² - m(m + 2)

= m² + 2m + 1 - m² - 2m

= 1 > 0

Phương trình luôn có hai nghiệm phân biệt

Theo hệ thức Vi-ét, ta có:

x₁ + x₂ = 2(m + 1)/m

x₁x₂ = (m + 2)/m

Câu 3:

∆' = 4 - (2 - √3)(2 + √2)

= 4 - 4 - 2√2 + 2√3 + √6

= √6 + 2√3 - 2√2 > 0

Phương trình luôn có hai nghiệm phân biệt

Theo hệ thức Vi-ét, ta có:

x₁ + x₂ = -4/(2 - √3)= -8 - 2√3

x₁x₂ = (2 + √2)/(2 - √3) = (2 + √2)(2 + √3)

Số trừ là số bé nhất có bốn chữ số nên là 1000

Hiệu là số lớn nhất có bốn chữ số nên là 9999

Số bị trừ là:

9999 + 1000 = 10999

Chiều rộng hình chữ nhật là:

100:4=25(cm)

Chu vi hình chữ nhật là:

(45+25)x2=70x2=140(cm)

Chiều rộng hình chữ nhật là:

\(100:4=25\left(cm\right)\)

Chu vi hình chữ nhật là:

\(\left(45+25\right)\times2=140\left(cm\right)\)

\(\dfrac{x-2}{3}=\dfrac{x+1}{4}\)

=>4(x-2)=3(x+1)

=>4x-8=3x+3

=>x=11

\(x+\dfrac{1}{3}=\dfrac{25}{-5}\)

\(x+\dfrac{1}{3}=-5\)

\(x=-5-\dfrac{1}{3}\)

\(x=-\dfrac{16}{3}\)

x + 1/3 = 25/-5

x + 1/3 = -5

x             = -5 - 1/3

x             = -16/3

D và E cùng nhìn BC dưới 1 góc vuông \(\Rightarrow BCDE\) nội tiếp

\(\Rightarrow\widehat{BDE}=\widehat{BCE}\) (cùng chắn BE)

Lại có \(\widehat{BCE}=\widehat{BD'E'}\) (cùng chắn BE' của (O))

\(\Rightarrow\widehat{BDE}=\widehat{BD'E'}\)

\(\Rightarrow DE||D'E'\) (hai góc đồng vị bằng nhau)

Pt hoành độ giao điểm: \(x^2=2x-m+3\) (1) 

\(\Leftrightarrow x^2-2x+m-3=0\)

\(\Delta'=1-\left(m-3\right)>0\Rightarrow m< 4\)

Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)

Do \(x_1\) là nghiệm của (1) nên: \(x_1^2=2x_1-m+3\)

Thế vào:

\(x_1^2+12=2x_2-x_1x_2\)

\(\Leftrightarrow2x_1-m+3+12=2x_1-\left(m-3\right)\)

\(\Leftrightarrow x_1-x_2=6\)

\(\Rightarrow x_2=x_1-6\)

Thế vào \(x_1+x_2=2\Rightarrow x_1+x_1-6=2\)

\(\Rightarrow x_1=4\Rightarrow x_2=-2\)

Thay vào \(x_1x_2=m-3\Rightarrow m-3=-8\)

\(\Rightarrow m=-5\) (thỏa mãn)