Lúc 8 giờ 25 phút một xe máy đi từ A với vận tốc 30 km/giờ. Đến 9 giờ kém 5 phút cùng ngày một ô tô cũng đi từ A với vận tốc 50 km/giờ cùng chiều với xe máy. Hỏi ô tô đuổi kịp xe máy lúc mấy giờ ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Số tập hợp con có 1 phần tử của P là \(C^1_4=4\left(tậphợp\right)\)
{1};{3};{6};{8}
b: Số tập hợp con có 3 phần tử của P là \(C^3_4=4\)(tập hợp)
Các tập hợp đó là {1;3;6}; {1;3;8}; {1;6;8}; {3;6;8}
c: Số tập hợp con của P là \(2^4=16\)(tập hợp)

Ta có: GH//JI
=>\(\widehat{JGH}+\widehat{GJI}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{JGH}=180^0-90^0=90^0\)
ta có: GH//JI
=>\(\widehat{HIJ}=\widehat{xHI}\)(hai góc so le trong)
=>\(\widehat{HIJ}=47^0\)

\(x^2\left(x-2\right)+3\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x^2+3\right)=0\)
mà \(x^2+3>=3>0\forall x\)
nên x-2=0
=>x=2

a: Xét ΔMNQ có
NE,MF là các đường cao
NE cắt MF tại H
Do đó: H là trực tâm của ΔMNQ
=>QH\(\perp\)MN tại D
Xét `ΔMQN` có:
Đường cao `NE` và `MF` cắt nhau tại H
`=> H` là trực tâm của `ΔMQN`
`=> QD` là đường cao của `ΔMQN` (đi qua H)
`=> QH ⊥ MN` tại `D`

Sửa đề:
`S = 1/3 + 2/(3^2) + 3/(3^3) + ... + 100/(3^100)`
`3S = 1 + 2/3 + 3/(3^2) + ... + 100/(3^99)`
`3S - S = 1 - 100/3^100 + (2/3 - 1/3) + (3/(3^2) - 2/(3^2)) + ... + (100/(3^99) - 99/(3^99)) `
`2S = 1 - 100/(3^100) + 1/3 + 1/(3^2) + ... + 1/(3^99) `
Đặt `A = 1/3 + 1/(3^2) + ... + 1/(3^99) `
`=> 3A = 1 + 1/3 + ... + 1/(3^98) `
`=> 3A - A = (1 + 1/3 + ... + 1/(3^98)) - ( 1/3 + 1/(3^2) + ... + 1/(3^99) )`
`=> 2A = 1 - 1/(3^99)`
`=> A = (1 - 1/(3^99))/2`
Khi đó: `2S = 1 - 100/(3^100) + (1 - 1/(3^99))/2`
`S = 1/2 - 100/(2.3^100) + (1 - 1/(3^99))/4`
Ta có: `{(1/2 - 100/(2.3^100) < 1/2),((1 - 1/(3^99))/4 < 1/4):}`
`=> 1/2 - 100/(2.3^100) + (1 - 1/(3^99))/4 < 1/2 + 1/4 = 3/4`
Hay `S < 3/4 (đpcm)`

Ông An cao 180 cm, vòng bụng 108 cm.
Ông Chung cao 160 cm, vòng bụng 70 cm.

Với mọi x;y dương ta có:
\(x^2+xy+y^2=\dfrac{3}{4}\left(x^2+2xy+y^2\right)+\dfrac{1}{4}\left(x^2-2xy+y^2\right)\)
\(=\dfrac{3}{4}\left(x+y\right)^2+\dfrac{1}{4}\left(x-y\right)^2\ge\dfrac{3}{4}\left(x+y\right)^2\)
Áp dụng:
\(P\ge\sqrt{\dfrac{3}{4}\left(a+b\right)^2}+\sqrt{\dfrac{3}{4}\left(b+c\right)^2}+\sqrt{\dfrac{3}{4}\left(c+a\right)^2}\)
\(P\ge\dfrac{\sqrt{3}}{2}\left(a+b\right)+\dfrac{\sqrt{3}}{2}\left(b+c\right)+\dfrac{\sqrt{3}}{2}\left(c+a\right)\)
\(P\ge\sqrt{3}\left(a+b+c\right)=\sqrt{3}\)
\(P_{min}=\sqrt{3}\) khi \(a=b=c=\dfrac{1}{3}\)

a: |2,5|+|7,5|=2,5+7,5=10
b: \(1,2\cdot\left|-3\right|+6,4=1,2\cdot3+6,4=3,6+6,4=10\)
c: \(\left|-\dfrac{7}{2}\right|+\left|\dfrac{15}{2}\right|=\dfrac{7}{2}+\dfrac{15}{2}=\dfrac{22}{2}=11\)

\(\left(3x-2^4\right)\cdot7^{13}=2\cdot7^{14}\)
=>\(3x-16=2\cdot\dfrac{7^{14}}{7^{13}}=2\cdot7=14\)
=>3x=16+14=30
=>\(x=\dfrac{30}{3}=10\)
\(\left(3x-2^4\right).7^{13}=2.7^{14}\\ \Rightarrow\left(3x-16\right).7^{13}=2.7.7^{13}\\ \Rightarrow3x-16=2.7\\ \Rightarrow3x-16=14\\ \Rightarrow3x=30\\ \Rightarrow x=30:3\\ \Rightarrow x=10\)
Vậy: \(x=10\)


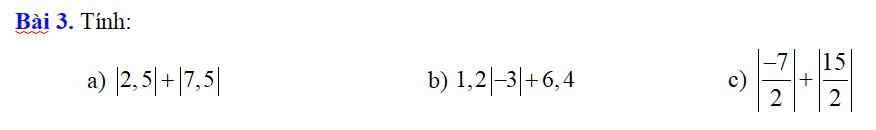
9h kém 5p=8h55p
8h55p-8h25p=30p=0,5 giờ
Sau 0,5 giờ, xe máy đi được:
30x0,5=15(km)
Hiệu vận tốc hai xe là 50-30=20(km/h)
Hai xe gặp nhau sau khi ô tô đi được:
15:20=0,75(giờ)=45p
Ô tô đuổi kịp xe máy lúc:
8h55p+45p=9h40p