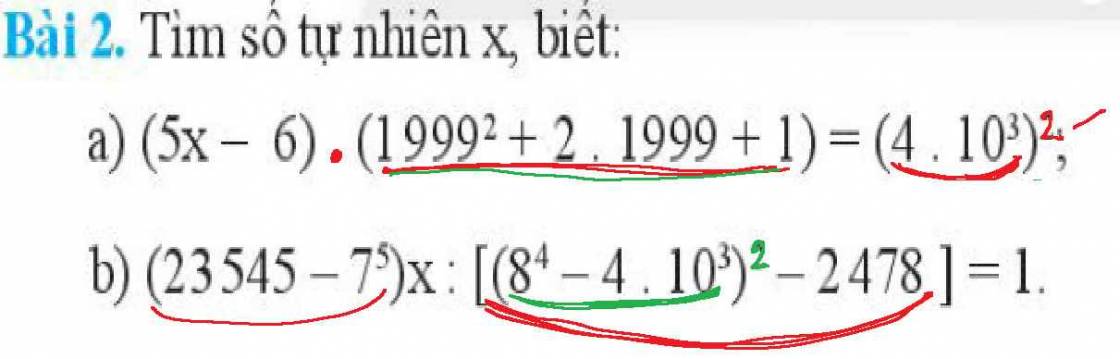 giúp em với giải thích từng bước giúp em ạ . Em cảm ơn
giúp em với giải thích từng bước giúp em ạ . Em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)5x +12 = 22
5x = 22 - 12
5x = 10
x = 2
2)45 : x + 100 =105
45 : x = 105 - 100
45 :x = 5
x = 45 : 5
x= 9
77-2.x =17
2.x = 77 - 17
2.x = 60
x = 60 :2
x= 30
88-18.x = 70
18.x = 88 - 70
18 .x = 18
x = 1

Gọi số thỏa mãn đề bài là \(x\) ( 1500 ≤ \(x\) ≤ 1800)
\(\left\{{}\begin{matrix}x-7⋮29\\x-15⋮31\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=29k +7\\29k+7-15⋮31\end{matrix}\right.\); k \(\in\) Z
⇒ \(\left\{{}\begin{matrix}1500\le29k+7\le1800\\29k-8⋮31\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}51,48\le k\le61,82\\29k-8-31k⋮31\end{matrix}\right.\) k \(\in\)Z
⇔ \(\left\{{}\begin{matrix}k\in\left\{52;53;...;61\right\}\\2k-8⋮31\end{matrix}\right.\) (1)
2k - 8 ⋮ 31 ⇔ k - 4 ⋮ 31 ⇔ k- 4 \(\in\) { 0; 31; 62; 93;...;}
k \(\in\) { -4; 27; 58; 79;...;} (2)
Kết hợp (1) và (2) ta có: k = 58
Thay k = 58 vào biểu thức 29k + 7 ta có
Số cần tìm là: 29.58 + 7 = 1689
Kết luận: số thỏa mãn đề bài là 1689
Thử lại kết quả ta có: 1500 < 1689 < 1800 (ok)
1689 : 29 = 58 dư 7 ok
1689 : 31 = 54 dư 15 ok
Vậy kết quả bài toán là đúng.

A = 11 x 13 x 15 x..x 99 - 12 x 14 x 16 ...x 98
B = 11 x 13 x 15 x... x 99 = \(\overline{..5}\)
C = 12 x 14 x 16 x...x 98 là số chẵn
B - C là số lẻ ( vì hiệu của số lẻ và số chẵn là một số lẻ)
A = B - C là một số lẻ \(\ne\) 100
Vậy A = 100 là sai
11 × 13 × 15 × ... × 99 - 12 × 14 × 16 × ... × 98 = 100 là sai vì:
11 × 13 × 15 × ... × 99 có chữ số tận cùng là chữ số lẻ
12 × 14 × 16 × ... × 98 có chữ số tận cùng là chữ số chẵn
Mà 100 có chữ số tận cùng là 0

Gọi số cần tìm là \(\overline{ab}\)
Ta có :
\(\overline{ab}+160=\overline{a7b}\)
a x 10 + b + 160 = a x 100 + 70 + b
160 -70 = a x100 + b -b - a x10
90 = 90a
a = 1 ; b = 0;1;2;3;4;5;6;7;8;9
các số thoả mãn đề bài là
10 ; 11 ; 12;13;14;15;16;17;`18;19

\(A=\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{61\cdot64}+\dfrac{3}{64\cdot67}\)
\(A=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{61}-\dfrac{1}{64}+\dfrac{1}{64}-\dfrac{1}{67}\)
\(A=1-\dfrac{1}{67}\) < 1
=> A<1
Ta có:
\(A=\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{61.64}+\dfrac{3}{64.67}\)
\(=3.\dfrac{1}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{61}-\dfrac{1}{64}+\dfrac{1}{64}-\dfrac{1}{67}\right)\)
\(=3.\left(1-\dfrac{1}{67}\right)\)
\(=3.\dfrac{66}{67}\)
\(=\dfrac{198}{67}\)
Vì \(\dfrac{198}{67}\) có tử lớn hơn mẫu nên \(\dfrac{198}{67}>1\)
Vậy \(A>1\)

Trong 1 giờ hai người cùng làm được: 1 : 4 = \(\dfrac{1}{4}\) (công việc)
Người thứ hai làm một mình trong một giờ được:
\(\dfrac{1}{3}\) : 2 = \(\dfrac{1}{6}\) (công việc)
Trong một giờ người thứ nhất làm một mình được:
\(\dfrac{1}{4}\) - \(\dfrac{1}{6}\) = \(\dfrac{1}{12}\) (công việc)
Nếu làm riêng người thứ nhất làm xong công việc sau:
1 : \(\dfrac{1}{12}\) = 12(giờ)
Nếu làm riêng người thứ hai làm xong công việc sau:
1 : \(\dfrac{1}{6}\) = 6 (giờ)
Đs..
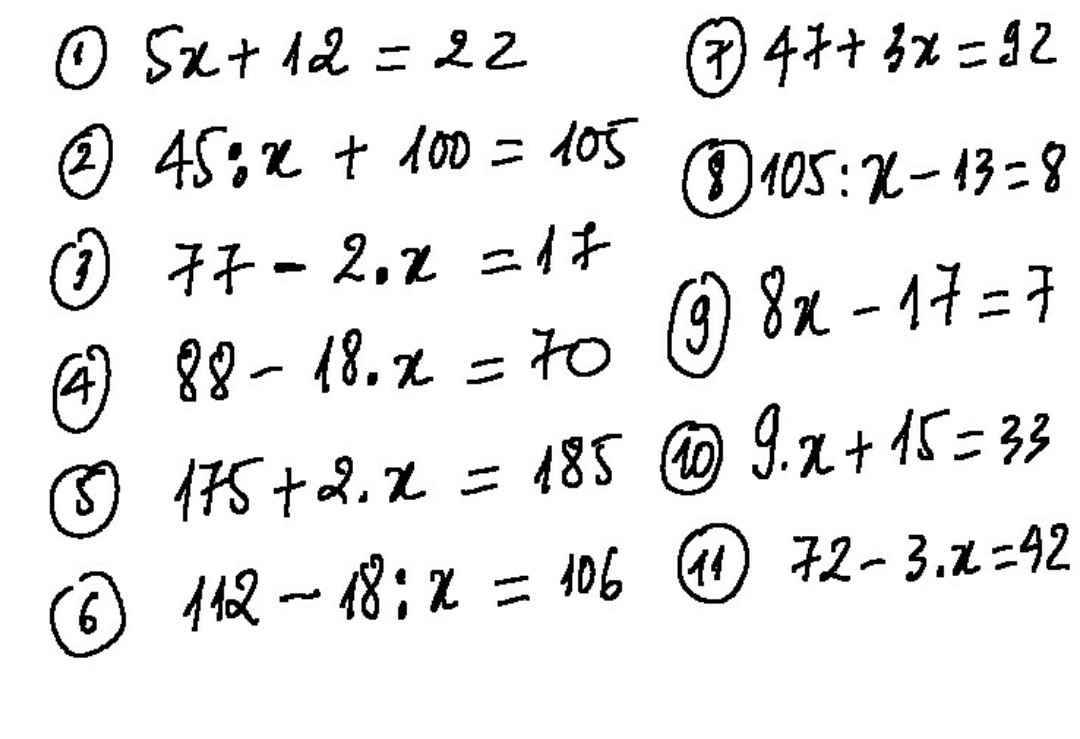
Lời giải:
a.
$(5x-6)(1999^2+2.1999+1)=4.10^3$
$(5x-6)(1999+1)^2=(4.10^3)^2=4000^2$
$(5x-6).2000^2=4000^2$
$5x-6=\frac{4000^2}{2000^2}=2^2=4$
$5x=10$
$x=10:5=2$
b.
$(23545-7^5)x:[(8^4-4.10^3)^2-2478]=1$
$6738.x:6738=1$
$x=1$