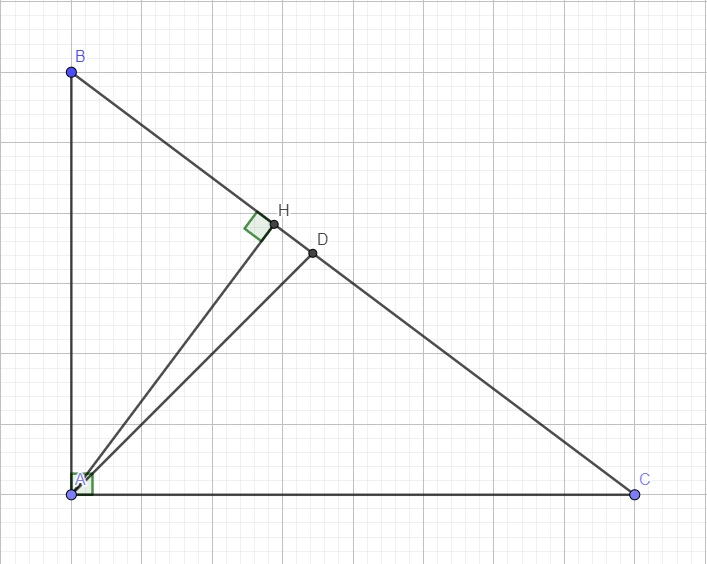
cho tam giác ABC vuông tại A , phân giác AD, đường cao AH . Biết BD =15 cm ,CD=20cm. Tính độ dài đoạn AH = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BD+CD=BC
=>BC=15+20=35(cm)
Xét ΔABC có AD là phân giác
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)
=>AB=3k; AC=4k
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)
=>\(25k^2=1225\)
=>\(k^2=49\)
=>k=7
=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
\(=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)

Ta có \(BC=BD+CD=35\left(cm\right)\)
Áp dụng định lý phân giác:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng định lý Pitago:
\(AB^2+AC^2=BC^2\Rightarrow\dfrac{9}{16}AC^2+AC^2=35^2\)
\(\Rightarrow AC^2=784\Rightarrow AC=28\left(cm\right)\)
\(\Rightarrow AB=\dfrac{3}{4}AC=21\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông ABC:
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{63}{5}\left(cm\right)\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\dfrac{84}{5}\left(cm\right)\)
\(HD=BD-BH=\dfrac{12}{5}\left(cm\right)\)
Áp dụng Pitago trong tam giác vuông ADH:
\(AD=\sqrt{AH^2+HD^2}=12\sqrt{2}\left(cm\right)\)

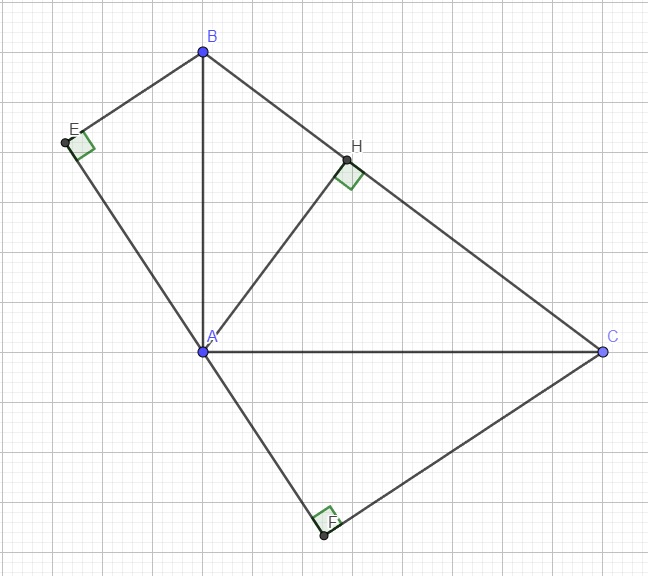
a.
Ta có: \(\widehat{BAE}+\widehat{BAC}+\widehat{CAF}=180^0\)
\(\Rightarrow\widehat{BAE}+90^0+\widehat{CAF}=180^0\)
\(\Rightarrow\widehat{BAE}+\widehat{CAF}=90^0\) (1)
Lại có \(BE\perp d\Rightarrow\Delta BAE\) vuông tại E
\(\Rightarrow\widehat{BAE}+\widehat{ABE}=90^0\) (2)
(1);(2) \(\Rightarrow\widehat{CAF}=\widehat{ABE}\)
Xét hai tam giác ABE và CAF có:
\(\left\{{}\begin{matrix}\widehat{ABE}=\widehat{CAF}\\\widehat{AEB}=\widehat{CFA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABE\sim\Delta CAF\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{CF}=\dfrac{BE}{AF}\Rightarrow AE.AF=BE.CF\)
b.
\(S_{ABC}=\dfrac{1}{2}AB.AC\Rightarrow AC=\dfrac{2S_{ABC}}{AB}=\dfrac{2.24}{6}=8\left(cm\right)\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{6.8}{\sqrt{6^2+8^2}}=4,8\left(cm\right)\)

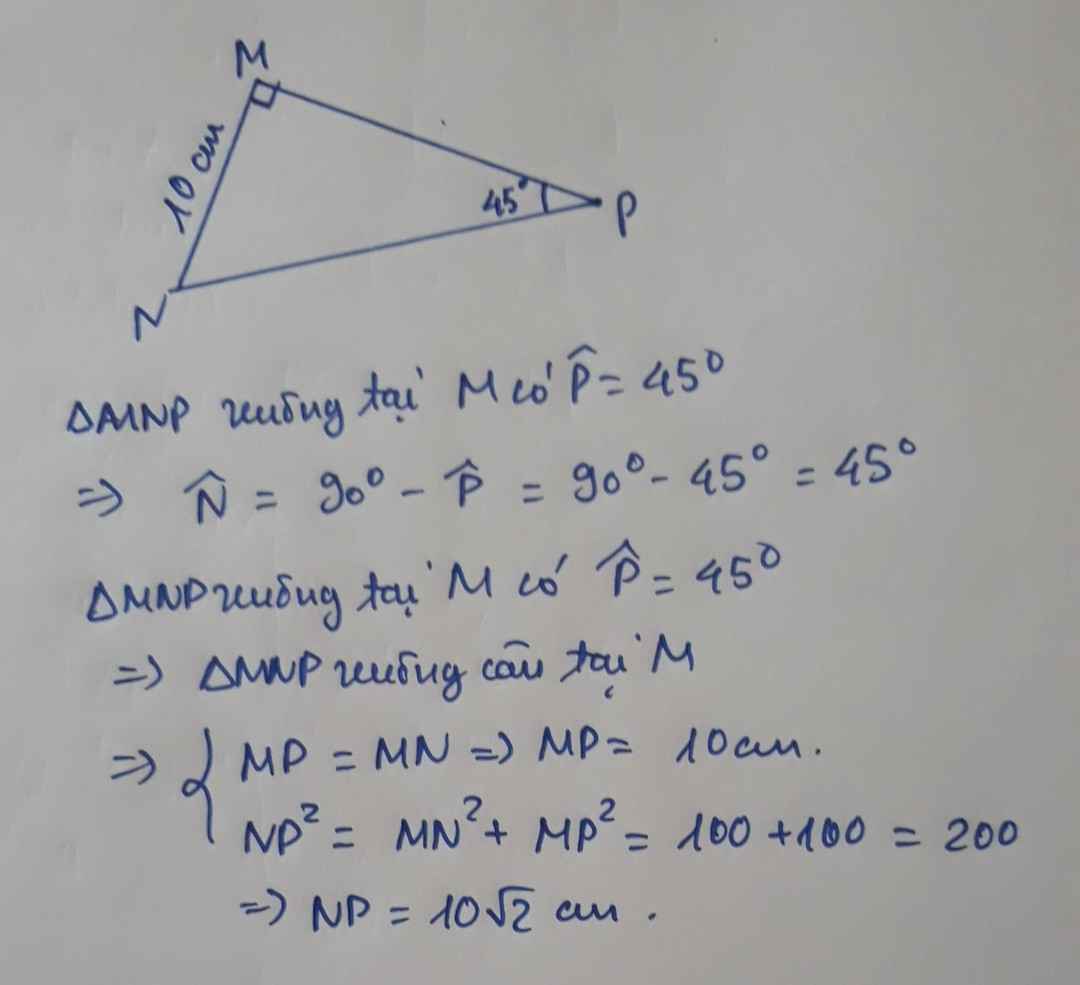
ΔMNP vuông tại M
=>\(\widehat{MNP}+\widehat{P}=90^0\)
=>\(\widehat{N}=90^0-45^0=45^0\)
Xét ΔMNP vuông tại M có \(tanP=\dfrac{MN}{MP}\)
=>\(\dfrac{10}{MP}=tan45=1\)
=>MP=10(cm)
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(NP=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)

\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{4+2\sqrt{3}}}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{4-2\sqrt{3}}}\)
\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{\left(\sqrt{3}+1\right)^2}}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{3}+1}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\left(\sqrt{3}-1\right)}=\sqrt{2}\left(\dfrac{2+\sqrt{3}}{3+\sqrt{3}}+\dfrac{2-\sqrt{3}}{3-\sqrt{3}}\right)\)
\(=\sqrt{2}\left(\dfrac{\left(2+\sqrt{3}\right)\left(3-\sqrt{3}\right)+\left(2-\sqrt{3}\right)\left(3+\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}\right)\)
\(=\sqrt{2}\left(\dfrac{6}{9-3}\right)=\sqrt{2}\)

Có \(a^4+b^4+c^4=\left(a^2\right)^2+\left(b^2\right)^2+\left(c^2\right)^2\)
\(\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{3}\)
\(\ge\dfrac{\left(\dfrac{\left(a+b+c\right)^2}{3}\right)^2}{3}\) (áp dụng 2 lần BĐT \(x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}\))
\(=\dfrac{\left(\dfrac{4^2}{3}\right)^2}{3}=\dfrac{256}{27}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=\dfrac{4}{3}\)
Vậy \(minP=\dfrac{256}{27}\) khi \(a=b=c=\dfrac{4}{3}\)
Min P dễ em có thể tự tìm đơn giản bằng AM-GM
\(P=\left(a^2+b^2+c^2\right)^2-2\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(=\left(a^2+b^2+c^2\right)^2-2\left(ab+bc+ca\right)^2+4abc\left(a+b+c\right)\)
\(=\left(a^2+b^2+c^2\right)^2-2\left(ab+bc+ca\right)^2+16abc\)
Do \(0\le a;b;c\le3\Rightarrow\left(3-a\right)\left(3-b\right)\left(3-c\right)\ge0\)
\(\Rightarrow3\left(ab+bc+ca\right)-9\left(a+b+c\right)+27-abc\ge0\)
\(\Rightarrow ab+bc+ca\ge\dfrac{abc+9}{3}\)
\(a^2+b^2+c^2=\left(a+b+c\right)^2-2\left(ab+bc+ca\right)=16-2\left(ab+bc+ca\right)\)
\(\le16-\dfrac{2}{3}\left(abc+9\right)\)
Do đó:
\(P\le\left[16-\dfrac{2}{3}\left(abc+9\right)\right]^2-2\left(\dfrac{abc+9}{3}\right)^2+16abc\)
Đặt \(abc=x\Rightarrow0\le x\le\dfrac{64}{27}\)
\(P\le\left[16-\dfrac{2}{3}\left(x+9\right)\right]^2-2\left(\dfrac{x+9}{3}\right)^2+16x\)
\(P\le\dfrac{2}{9}\left(x^2-6x+369\right)\)
\(P\le\dfrac{2}{9}x\left(x-6\right)+82\)
Do \(0\le x\le\dfrac{64}{27}\Rightarrow x-6< 0\Rightarrow\dfrac{2}{9}x\left(x-6\right)\le0\)
\(\Rightarrow P\le82\)
Dấu "=" xảy ra khi \(x=0\) hay \(\left(a;b;c\right)=\left(0;1;3\right)\) và các hoán vị

Đề yêu cầu chứng minh hay tìm \(x;y\) vậy em nhỉ?

Gọi số cần tìm là \(\overline{xy}\) với x;y là các chữ số từ 0 tới 9, `x \ne 0`
Do tổng chữ số hàng chục và 2 lần chữ số hàng đơn vị là 12 nên ta có:
\(x+2y=12\) (1)
Sau khi thêm chữ số 0 vào giữa ta được số mới là: \(\overline{x0y}\)
Do số mới hơn số cũ 180 đơn vị nên ta có pt:
\(\overline{x0y}-\overline{xy}=180\Leftrightarrow100x+y-\left(10x+y\right)=180\)
\(\Leftrightarrow90x=180\)
\(\Leftrightarrow x=2\)
Thay vào (1) \(\Rightarrow2+2y=12\Rightarrow y=5\)
Vậy số đó là 25
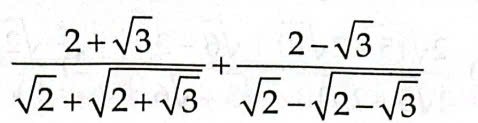
BD+CD=BC
=>BC=15+20=35(cm)
Xét ΔABC có AD là phân giác
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)
=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)
=>AB=3k; AC=4k
Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)
=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)
=>\(25k^2=1225\)
=>\(k^2=49\)
=>k=7
=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH=\dfrac{21\cdot28}{35}=21\cdot\dfrac{4}{5}=16,8\left(cm\right)\)