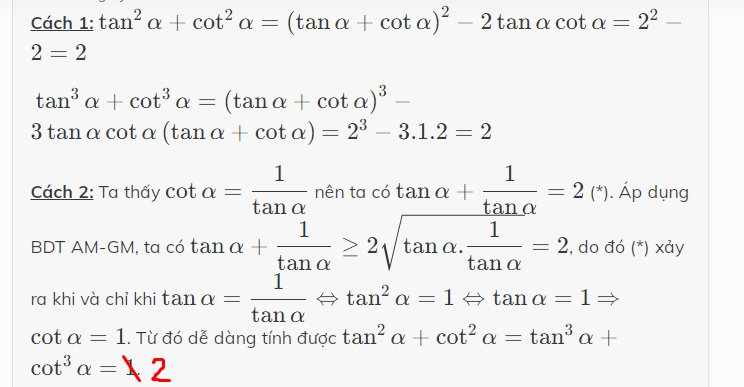Cho tanα+cotα=2
Tính tan^2α+cot^2α;tan^3α+cot^3α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.

Ta có : \(x^4+2x^3-10x^2+10x-3=y^2\)
\(\Leftrightarrow\left(x^4+2x^3-3\right)-\left(10x^2-10x\right)=y^2\)
\(\Leftrightarrow\left(x-1\right).\left(x^3+3x^2-7x+3\right)=y^2\)
\(\Leftrightarrow\left(x-1\right)^2.\left(x^2+4x-3\right)=y^2\)
Vì \(x,y\inℤ\) nên y2 là số chính phương khi
x2 + 4x - 3 là số chính phương
Đặt x2 + 4x - 3 = t2
\(\Leftrightarrow\left(x+t+2\right).\left(x-t+2\right)=7\)
Ta có bảng
| x + t + 2 | 1 | 7 | -1 | -7 |
| x - t + 2 | 7 | 1 | -7 | -1 |
| x | 2 | 2 | -6 | -6 |
| t | -3 | 3 | 3 | -3 |
Ta được x = 2 ; x = -6 thỏa
Với x = 2 <=> y = \(\pm3\)
Với x = -6 <=> y = \(\pm21\)

\(c,\dfrac{3\sqrt{x}-6}{7\sqrt{x}-3}=\dfrac{1}{6}\left(dk:x\ge0,x\ne\dfrac{9}{49}\right)\)
\(\Leftrightarrow\dfrac{6\left(3\sqrt{x}-6\right)-7\sqrt{x}+3}{6\left(7\sqrt{x}-3\right)}=0\)
\(\Leftrightarrow18\sqrt{x}-36-7\sqrt{x}+3=0\)
\(\Leftrightarrow11\sqrt{x}=33\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\left(tmdk\right)\)
Vậy \(S=\left\{9\right\}\)
\(d,\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{1}{3}\left(dk:x\ne9,x\ge0\right)\)
\(\Leftrightarrow\dfrac{3\left(2\sqrt{x}+1\right)-\sqrt{x}+3}{3\left(\sqrt{x}-3\right)}=0\)
\(\Leftrightarrow6\sqrt{x}+3-\sqrt{x}+3=0\)
\(\Leftrightarrow5\sqrt{x}=-6\)
\(\Leftrightarrow\sqrt{x}=-\dfrac{6}{5}\left(ktm\right)\)
Vậy \(S=\varnothing\)
\(\dfrac{3\sqrt{x}-6}{7\sqrt{x}-3}=\dfrac{1}{6}\left(x\ge0\right) \\ \Leftrightarrow6\left(3\sqrt{x}-6\right)=7\sqrt{x}-3\\ \Leftrightarrow18\sqrt{x}-36=7\sqrt{x}-3\\ \Leftrightarrow18\sqrt{x}-7\sqrt{x}=-3+36\\ \Leftrightarrow11\sqrt{x}=33\\ \Leftrightarrow\sqrt{x}=\dfrac{33}{11}=3\\ x=3^2=9\\ Vậy:S=\left\{9\right\}\)

\(C=\sqrt{14-8\sqrt{3}}-\sqrt{21-12\sqrt{3}}\)
\(=\sqrt{2\left(7-4\sqrt{3}\right)}-\sqrt{12-2\cdot2\sqrt{3}\cdot3+9}\)
\(=\sqrt{2}\cdot\sqrt{4-2\cdot2\cdot\sqrt{3}+3}-\sqrt{\left(\sqrt{12}-3\right)^2}\)
\(=\sqrt{2}\cdot\sqrt{\left(2-\sqrt{3}\right)^2}-\left|2\sqrt{3}-3\right|\)
\(=\sqrt{2}\cdot\left|2-\sqrt{3}\right|-\left(2\sqrt{3}-3\right)\) (vì \(2\sqrt{3}-3>0\) )
\(=\sqrt{2}\cdot\left(2-\sqrt{3}\right)-2\sqrt{3}+3\) (vì \(2-\sqrt{3}>0\) )
\(=2\sqrt{2}-\sqrt{6}-2\sqrt{3}+3\)

Gọi \(q_1,q_2,...,q_n\left(q_i\inℚ,\forall i=\overline{1,n}\right)\). Theo đề bài, ta có \(q_1q_2...q_n\inℤ\) và \(q_i+q_j\inℤ,\forall i\ne j;i,j=\overline{1,n}\). Không mất tính tổng quát, giả sử \(q_1< q_2< ...< q_n\)
Ta thấy \(q_1+q_2\inℤ\) và \(q_2+q_3\inℤ\) nên \(q_1-q_3\inℤ\). Mà \(q_1+q_3\inℤ\) nên nếu ta đặt \(q_1-q_3=v\) và \(q_1+q_3=u\) với \(u,v\inℤ\) thì \(q_1=\dfrac{u+v}{2};q_3=\dfrac{u-v}{2}\). Do \(q_1+q_2=\dfrac{u+v+2q_2}{2}\) và \(q_3+q_2=\dfrac{u-v+2q_2}{2}\) cũng là các số nguyên, hơn nữa \(u-v\equiv u+v\left(mod2\right)\) nên ta chỉ cần suy ra \(u+v+2q_1⋮2\) hay \(u+v\) là số chẵn, cũng tức là \(q_1=\dfrac{u+v}{2}\) là số nguyên. Một cách tương tự, ta sẽ chứng minh được \(q_i\inℤ,\forall i=\overline{1,n}\) (đpcm)
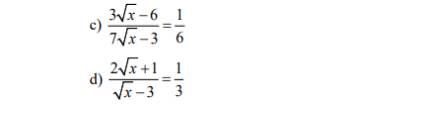

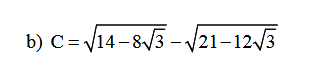
Cách 1: \(\tan^2\alpha+\cot^2\alpha=\left(\tan\alpha+\cot\alpha\right)^2-2\tan\alpha\cot\alpha\) \(=2^2-2=2\)
\(\tan^3\alpha+\cot^3\alpha=\left(\tan\alpha+\cot\alpha\right)^3-3\tan\alpha\cot\alpha\left(\tan\alpha+\cot\alpha\right)\) \(=2^3-3.1.2=2\)
Cách 2: Ta thấy \(\cot\alpha=\dfrac{1}{\tan\alpha}\) nên ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}=2\) (*). Áp dụng BDT AM-GM, ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}\ge2\sqrt{\tan\alpha.\dfrac{1}{\tan\alpha}}=2\), do đó (*) xảy ra khi và chỉ khi \(\tan\alpha=\dfrac{1}{\tan\alpha}\Leftrightarrow\tan^2\alpha=1\Leftrightarrow\tan\alpha=1\) \(\Rightarrow\cot\alpha=1\). Từ đó dễ dàng tính được \(\tan^2\alpha+\cot^2\alpha=\tan^3\alpha+\cot^3\alpha=2\).
(Tuyệt đối không được dùng cách 2 khi \(\tan\alpha\) hoặc \(\cot\alpha\) âm nhé, vì bất đẳng thức AM-GM chỉ dùng cho số dương thôi.)
Chỗ này phải sửa thành 2 mới đúng nhé.