Giúp mình với ạ. Đề bài là : điền dấu x vào ô thích hợp. Bài trên cùng nha. 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`3/7 + (-5/2) + (-3/5)`
`=3/7 - 5/2 - 3/5`
`=30/70 - 175/70 - 42/70`
`=(30-175-42)/70`
`=(-187)/70`
___________________________________
`(-4/3) + (-2/5) + (-3/2)`
`=(-4/3) - 2/5 - 3/2`
`=(-40/30) - 12/30 - 45/30`
`=(-40 - 12 - 45)/30`
`=(-97)/30`
\(a.\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{5}\right)=\dfrac{3}{7}-\dfrac{5}{2}-\dfrac{3}{5}=\dfrac{30-175-42}{70}=-\dfrac{187}{70}\\ b.-\dfrac{4}{3}+\left(-\dfrac{2}{5}\right)+\left(-\dfrac{3}{2}\right)=-\dfrac{4}{3}-\dfrac{2}{5}-\dfrac{3}{2}=\dfrac{-40-12-45}{30}=\dfrac{-97}{30}\)

\(\dfrac{25^4}{5^3}=\dfrac{\left(5^2\right)^4}{5^3}=\dfrac{5^8}{5^3}=5^5\)

430 = (44)7.42 = \(\overline{...6}\)7 . 16 = \(\overline{...6}\)
981 = (92)40.9 = \(\overline{...1}\)40.9 = \(\overline{...9}\)
1833 = (184)8.18 = \(\overline{....6}\)8.18 = \(\overline{....8}\)
232023 = (234)505.233 = \(\overline{....1}\)505.\(\overline{....7}\)= \(\overline{....7}\)

\(\left(a-b-c\right)-\left(a-c\right)=a-b-c-a+c=-b\\ \left(a+b\right)-\left(-a+b-c\right)=a+b+a-b+c=2a+c\\ -\left(a+b\right)+\left(a+b+c\right)=-a-b+a+b+c=c\\ \left(a+b-c\right)-\left(a-c\right)=a+b-c-a+c=b\\ \left(a+b\right)+\left(a-c-d+b\right)=a+b+a-c-d+b=2a+2b-c-d\\ -\left(a-b+c\right)+\left(a-b+d\right)=-a+b-c+a-b+d=-c+d\)
b, =a-b-c-a+c=-b
b, =a+b+a-b+c=2a+c
b, =-a-a+a+b+c=a+b+c
c,= a+b-c-a+c=2a+b
c, =a+b+a-c-d+b=2a+2b-c-d
c, =-a+b-c+a-b+d=-c+d

ctv olm có mặt nhé ! ố ồ bài này là đề thi học sinh giỏi toán lớp 6 cấp huyện Đông Hưng vòng 4
vì số tự nhiên đó chia 9 dư 5 , chia 7 dư 3 nên khi ta thêm 4 vào số tự nhiên đó thì số đó trở thành số chia hết cho cả 7 và 9 vậy số tự nhiên lúc sau là bội của 7 và 9
BCNN(7, 9) = 7 x 9 = 63
số tự nhiên lúc sau có dạng 63k với k \(\in\) N*
⇒ số tự nhiên chia 7 dư 3, chia 9 dư 5 có dạng 63k - 4
63k - 4 = 63. (k- 1+1) -4
⇔63k - 4 = 63(k-1) + 63 - 4
⇔ 63k - 4 = 63(k-1) + 59
mà 63.(k-1) ⋮ 63 ∀ k \(\in\) N*
⇔ 63 . (k-1) + 59 : 63 dư 59
⇔ 63k - 4 : 63 dư 59
kết luận...... bạn tự ghi nhé

Đáp án
\(\dfrac{\text{2005 x 2004 - 1}}{\text{2003 x 2005 + 2004}}\)
= 1
#hoctot
Tick cho mình nếu thấy đúng nhé

\(A=1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2017}-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(=1+\dfrac{1}{2}-\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{4}+...+2017+\dfrac{1}{2018}-\dfrac{1}{2018}-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2018}-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2018}-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2018}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2018}-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1009}\right)\)
\(=\dfrac{1}{1010}+\dfrac{1}{1011}+...+\dfrac{1}{2018}=B\)
\(\Rightarrow A=B\Rightarrow\left(A^{2022}-B^{2022}\right)^{2023}=0\)

Câu 3:
a. Vì $\overline{2a3b}\vdots 90$ nên nó cũng chia hết cho $10$
Do đó $b=0$
$\overline{2a30}\vdots 90$ nên nó cũng chia hết cho $9$
$\Rightarrow 2+a+3+0\vdots 9$
Hay $5+a\vdots 9$
Vì $a$ là số tự nhiên có 1 chữ số nên $a=4$
Vậy số cần tìm là $2430$
b.
Một số chính phương sẽ có dạng $a^2$ với $a$ là 1 số tự nhiên
Nếu $a$ chẵn, $a\vdots 2$ nên $a^2=a.a$ chia hết cho $4$, hay $a^2$ chia $4$ dư $0$
Nếu $a$ lẻ. Đặt $a=2k+1$ với $k$ tự nhiên. Khi đó:
$a^2=(2k+1)^2=4k^2+4k+1=4(k^2+k)+1$ chia $4$ dư $1$
Vậy $a^2$ chia $4$ có dư $0$ hoặc $1$
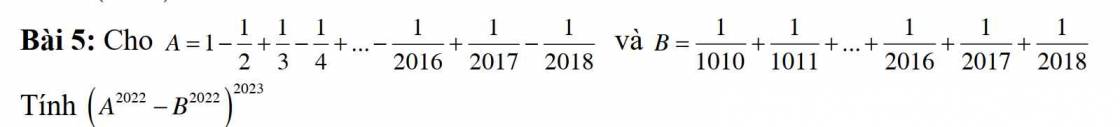

1S
2Đ
3Đ
4Đ
5Đ
6S
7Đ
8Đ
9S
10S
1S 2Đ
3Đ. 4Đ
5. S 6S
7. Đ 8Đ
9.S 10S