Dây dẫn được nối bằng các cách sau,mối nối thẳng,phân nhánh (rẽ), mối nối phụ kiện, mối nối cần phải hàn nhờ đó có thể

-Tăng tính thẩm mĩ của mối nối

-Tăng tuổi thọ của mối nối

Dây dẫn được nối bằng các cách sau,mối nối thẳng,phân nhánh (rẽ), mối nối phụ kiện, mối nối cần phải hàn nhờ đó có thể

-Tăng tính thẩm mĩ của mối nối

-Tăng tuổi thọ của mối nối

-Tăng tính dẫn điện của mối nối

-Giảm diện năng hao phí

-Tăng độ ăn toàn điện

-Tăng độ bền cơ học

Mối nối được bọc cách điện nhờ đó có thể,tăng tính thẩm mĩ của mối nối, tăng tuổi thọ của mối nối,tăng độ an toàn điện 

Diện tích của hình vành là:

3,14 x ( 1,5² - 1²) = ....... ( cm²)

Đ/s: ...... cm²

=3,925cm2

sau này chỉ có làm thì mới có ăn,còn cái loại mà ko tự làm thỉ chỉ có ăn đầu b**i , ăn c*t

Chiều cao của hình trụ là:

439,6 : 2 : 7 = 31,4 ( cm)

Đ/s: 31,4 cm

giải pt (1) ta có:

\(\sqrt{2x-y-1}\)- \(\sqrt{x+2y}\)+ \(\sqrt{3y+1}\)- \(\sqrt{x}\)=0

\(\frac{2x-y-1-x-2y}{\sqrt{2x-y-1}+\sqrt{x+2y}}\)+\(\frac{3y+1-x}{\sqrt{3y+1}+\sqrt{x}}\)=0

(x-3y-1)(\(\frac{1}{\sqrt{2x-y-1}+\sqrt{x+2y}}\)- \(\frac{1}{\sqrt{3y+1}+\sqrt{x}}\))

=> x=3y+1 thay vào (2) => x=1; y=0

trường hợp 2:

\(\frac{1}{\sqrt{2x-y-1}+\sqrt{x+2y}}\)=\(\frac{1}{\sqrt{3y+1}+\sqrt{x}}\)

=> \(\sqrt{3y+1}+\sqrt{x}\)=\(\sqrt{x+2y}+\sqrt{2x-y-1}\)

=> \(\sqrt{x}\)- \(\sqrt{2x-y-1}\)+ \(\sqrt{3y+1}\)- \(\sqrt{x+2y}\)=0

=> \(\frac{x-2x+y+1}{\sqrt{x}+\sqrt{2x-y-1}}\)+\(\frac{3y+1-x-2y}{\sqrt{3y+1}+\sqrt{x+2y}}\)=0

=>(-x + y + 1)(\(\frac{1}{\sqrt{x}+\sqrt{2x-y-1}}\)+ \(\frac{1}{\sqrt{3y+1}+\sqrt{x+2y}}\))=0

mà \(\frac{1}{\sqrt{x}+\sqrt{2x-y-1}}\)+\(\frac{1}{\sqrt{3y+1}+\sqrt{x+2y}}\)>0

=> x=y+1 thay vào 2 => \(\hept{\begin{cases}x=1\\y=0\end{cases}}\)

để đấy ku

Chỉ cần bỏ chữ cmr là đc

làm hộ mn với,vì đây là đề dành cho học sinh giỏi,mn sao chép về

132-79=

ta có :

\(\frac{a^3+b^3}{a^2+ab+b^2}=\frac{2a^3}{a^2+ab+b^2}+\frac{b^3-a^3}{a^2+ab+b^2}=\frac{2a^3}{a^2+ab+b^3}+b-a\)

tương tự rồi cộng theo vế : 

\(LHS\ge2\left(\frac{a^3}{a^2+ab+b^2}+\frac{b^3}{b^2+bc+c^2}+\frac{c^3}{c^2+ca+a^2}\right)\)

áp dụng bđt cô si

 \(\frac{a^3}{a^2+ab+b^2}+\frac{a^2+ab+b^2}{9}+\frac{1}{3}\ge\frac{3a}{3}=a\)

tương tự rồi cộng theo vế 

\(2\left(\frac{a^3}{a^2+ab+b^2}+...\right)\ge a+b+c-1-\frac{2\left(a^2+b^2+c^2+ab+bc+ca\right)}{9}\)

\(\ge\frac{2\left(9-a^2-b^2-c^2-ab-bc-ca\right)}{9}\)

đến đây chịu :)))))

giải:

Vẽ OH⊥EFOH⊥EF.

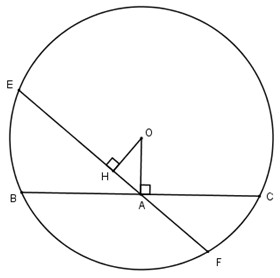
Xét tam giác HOA vuông tại H ta có:

OH<OAOH<OA.

Suy ra EF>BC.EF>BC.

Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

Kẻ $OH\perp EF$.

Trong tam giác $OHA$ vuông tại $H$, ta có:

$OA>OH$

Suy ra $BC<EF$

a) Trong đường tròn nhỏ:

AB > CD => OH < OK (định lí 3)

b) Trong đường tròn lớn:

OH < OK => ME > MF (định lí 3)

c) Trong đường tròn lớn:

ME > MF => MH > MK

a) Xét trong đường tròn nhỏ:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.

Theo giả thiết $AB>CD$ suy ra $AB$ gần tâm hơn, tức là  $OH<OK$.

b) Xét trong đường tròn lớn:

Theo định lí $2$: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.

Theo câu $a$, ta có: $OH<OK\Rightarrow ME>MF$.

c) Xét trong đường tròn lớn:

Vì $OH\perp ME\Rightarrow EH=MH=\frac{ME}{2}$ (Định lý 2 - trang 103).

Vì $OK\perp MF\Rightarrow KF=MK=\frac{MF}{2}$ (Định lý 2 - trang 103). 

Theo câu $b$, ta có: $ME>MF\Rightarrow \frac{ME}{2}>\frac{MF}{2}\iff MH>MK$

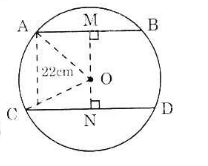
Kẻ OM ⊥ AB, ON ⊥ CD.

Ta thấy M, O, N thẳng hàng. Ta có:

Áp dụng định lí Pitago trong tam giác vuông AMO có:

OM² = OA² – AM² = 25² – 20² = 225

=> OM = √225 = 15cm

=> ON = MN – OM = 22 – 15 = 7 (cm)

Áp dụng định lí Pitago trong tam giác vuông CON có:

CN² = CO² – ON² = 25² – 7² = 576

=> CN = √576 = 24

=> CD = 2CN = 48cm

Ta tính được khoảng cách $OH$ từ $O$ đến $AB$ bằng $15$cm. Gọi $K$ là giao điểm của $HO$ và $CD$. Do $CD//AB$ nên $OK\perp CD$. Ta có:

$OK=HK-OH=22-15=7$(cm)

Từ đó tính được $CD=48$cm