Câu 3: Tâm của đường tròn ( O) tiếp xúc với 2 cạnh đường  Ay , Ax nằm trên đường phân giác OA
 

Gọi $O$ là tâm của một đường tròn bất kì tiếp xúc với hai cạnh của góc $xAy$.

Khi đó, \widehat{OAx}=\widehat{OAy}OAx=OAy​

Vậy tâm của các đường tròn tiếp xúc với hai cạnh của góc $xAy$ nằm trên tia phân giác của góc $xAy$.

 Ta có

DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)

\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)

\(=AB+AC=2AB\)

Theo tính chất hai tiếp tuyến cắt nhau ta có: $DM=DB,EM=EC$.

Chu vi tam giác $ADE$ bằng :

$AD+DE+AE=AD+DM+ME+EA$

$=AD+DB+EC+AE$

$=AB+AC=2.AB$ .

Bạn tự vẽ hình nha

a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.

Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)

b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).

Xét ΔCBD có :

CI = IB

CO = OD (bán kính)

⇒ BD // OI (OI là đường trung bình của tam giác BCD).

Vậy BD // AO.

c) Theo định lí Pitago trong tam giác vuông OAC:

AC^2 = OA^2 – OC^2 = 42 – 22 = 12

=> AC = √12 = 2√3 (cm)

\(\sin OAC=\frac{OC}{OA}=\frac{1}{2}\)

=> OAC =30 độ

mà BAC =2OAC

=. BAC =60

Tam giác ABC cân có BAC = 60 => Tam giác ABC đều

+> AB=AC=BC=2√3 (cm)

K cho mk nh

câu A : AB = AC ( theo tính chất của đường tiếp tuyến ) suy ra : tam giác ABC cân tại A , OA là đường phân giác cũng là đường cao vậy OA vuông góc với BC

Quốc hội Việt Nam khóa VI (1976-1981) Quốc hội đầu tiên của nước Việt Nam thống nhất được bầu vào ngày 25 tháng 4 năm 1976 với 492 đại biểu trúng cử. Cuộc bầu cử Quốc hội khóa VI cũng chính là cuộc Tổng tuyển cử để thống nhất Việt Nam theo các điều khoản trong Hiệp định Paris 1973

Quốc hội Việt Nam khóa VI (1976-1981) Quốc hội đầu tiên của nước Việt Nam thống nhất được bầu vào ngày 25 tháng 4 năm 1976 với 492 đại biểu trúng cử. Cuộc bầu cử Quốc hội khóa VI cũng chính là cuộc Tổng tuyển cử để thống nhất Việt Nam theo các điều khoản trong Hiệp định Paris 1973^[2]

^{* Nguồn :}  Quốc hội Việt Nam khóa VI – Wikipedia tiếng Việt

#Ninh Nguyễn

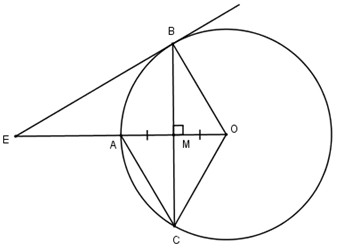
\(a,\) Tứ giác \(OCAB\)l là hình thoi.

Ta có: \(OA\perp OB\)\(\Rightarrow\)\(MB=MC\)

mà \(MA=MO\)nên tứ giác \(OCAB\)là hình bình hành.

Hình bình hành này có hai đường chéo vuông góc nên là hình thoi.

\(b,\) Ta có: \(BA=BO\) ( hai cạnh hình thoi ) \(BO=OA\)( bán kính tam giác ) nên tam giác \(ABO\)là tam giác đều.

\(\Rightarrow\)\(\widehat{BOA}=60^o\)

Ta có \(EB\)là tiếp tuyến \(\Rightarrow\)\(EB\perp OB\)

Xét tam giác \(BOE\)vuông tại \(B,\)có: 

\(BE=BO.tg60^o=R.tg60^o=R\sqrt{3}\)

a) Bán kính $OA$ vuông góc với dây $BC$ nên

$MB=MC$

Tứ giác $OCAB$ là hình bình hành (vì $MO=MA$, $MB=MC$), lại có $OA\perp BC$ nên tứ giác đó là hình thoi.

b) BE=Căn 3 x R

Dirichlet à:))?

Trong 3 số dương a,b,c tồn tại ít nhất 2 số cùng nhỏ hơn hoặc không nhỏ hơn 1

G/s 2 số đó là a và b

Khi đó: \(\left(1-a\right)\left(1-b\right)\ge0\Leftrightarrow ab-a-b+1\ge0\)

\(\Leftrightarrow ab\ge a+b-1\Leftrightarrow2abc\ge2ca+2bc-2c\)

\(\Rightarrow a^2+b^2+c^2+2abc+1\ge a^2+b^2+c^2+2ca+2bc-2c+1\)

Mà \(\left(a^2+b^2+c^2+2ca+2bc-2c+1\right)-2\left(ab+bc+ca\right)\)

\(=\left(a^2-2ab+b^2\right)+\left(c^2-2c+1\right)=\left(a-b\right)^2+\left(c-1\right)^2\ge0\left(\forall a,b,c\right)\)

\(\Rightarrow a^2+b^2+c^2+2ca+2bc-2c+1\ge2\left(ab+bc+ca\right)\)

\(\Rightarrow a^2+b^2+c^2+2abc+1\ge2\left(ab+bc+ca\right)\)

Dấu "=" xảy ra khi: a = b = c = 1

Theo nguyên lý Dirichlet, ta thấy rằng trong ba số a,b,c sẽ có hai số hoặc cùng ≥1 hoặc cùng ≤1. Giả sử hai số đó là a,b khi đó:
(a−1)(b−1)≥0.
Từ đây, bằng cách sử dụng hằng đẳng thức:
a2+b2+c2+2abc+1−2(ab+bc+ca)=(a−b)2+(c−1)2+2c(a−1)(b−1)≥0
Ta thu được ngay bất đẳng thức (1), phép chứng minh hoàn tất.

Search mạng!!

Lời giải:

a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:

Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)

⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)

b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm

OC=25cm

cùng chiều

Cùng chiều kim đồng hồ

Tâm $O$ là giao điểm của đường vuông góc với $d$ tại $A$ và đường trung trực của $AB$. Dựng đường tròn $(O;OA)$.

Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A. Suy ra tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.

Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.

Tam giác $ABC$ có:

AB^2+AC^2=3^{2}+4^{2}=5^{2}AB2+AC2=32+42=52

Mặt khác: BC^{2}=5^{2}BC2=52

Vậy \mathrm{AB}^{2}+\mathrm{AC}^{2}=\mathrm{BC}^{2}AB2+AC2=BC2.

Do đó \widehat{BAC}=90^{\circ}BAC=90∘ (định lí Py-ta-go đảo).

$CA$ vuông góc với bán kính $BA$ tại $A$ nên $CA$ là tiếp tuyến của đường tròn $(B)$.

tam giác ABC