\(A=2.5+5.8+8.11+...+293.296+296.299\\ 9A=2.5.9+5.8.9+8.11.9+...+293.296.9+296.299.9\\ 9A=2.5.9+5.8.\left(11-2\right)+8.11.\left(14-5\right)+...+293.296.\left(299-290\right)+296.299.\left(302-293\right)\)\(9A=2.5.9+5.8.11-2.5.8+8.11.14-5.8.11+...+293.296.299-290.293.296+296.299.302-293.296.299\)\(9A=2.5.9-2.5.8+296.299.302\\9A=10+296.299.302 \\ A=\dfrac{10+296.299.302}{9}=2969802\)

 Biểu thức đại số biều thị quãng đường đi của ô tô là : 30.x

Biểu thức biểu thị quãng đường là : \(s=30t\left(km\right)\)

Sửa đề: Chiều rộng là x (m)

Do chiều dài gấp đôi chiều rộng nên chiều dài là 2x (m)

Diện tích hình chữ nhật là:

2x.x = 2x² (m²)

A B C H I E F

a/

Xét tg ABI và tg ACI có

AB=AC (cạnh bên tg cân)

\(\widehat{BAH}=\widehat{CAH}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)

AI chung

=> tg ABI = tg ACI (c.g.c) => IB=IC => tg IBC cân

b/

tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{AIB}=\widehat{AIC}\)

c/ Xét tg IBF và tg ICE có

\(\widehat{BIF}=\widehat{CIE}\) (góc đối đỉnh)

IB=IC (cmt)

tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{ABI}=\widehat{ACI}\)

=> tg IBF = tg ICE => IE=IF

d/

Ta có

IE=IF (cmt) => tg IEF cân tại I

\(\Rightarrow\widehat{IEF}=\widehat{IFE}=\dfrac{180^o-\widehat{FIE}}{2}\) (1)

Xét tg cân IBC có

\(\widehat{IBC}=\widehat{ICB}=\dfrac{180^o-\widehat{BIC}}{2}\) (2)

Mà \(\widehat{FIE}=\widehat{BIC}\) (góc đối đỉnh) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{IFE}=\widehat{ICB}\) Hai góc này nằm ở vị trí so le trong

=> EF//BC

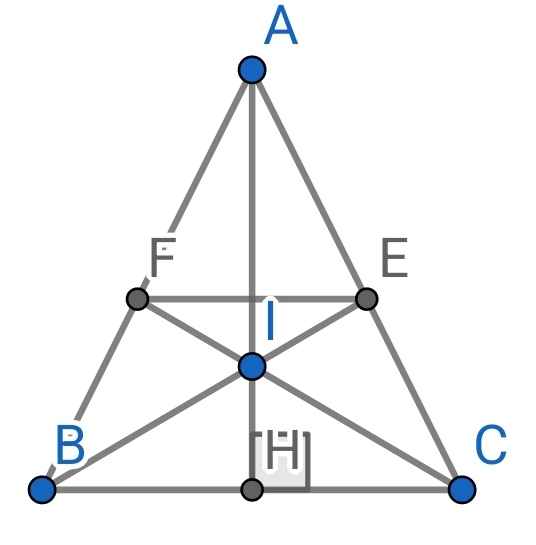 a) ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung trực của ∆ABC

⇒ AH là đường trung trực của BC

I ∈ AH (gt)

⇒ IB = IC

⇒ ∆IBC cân tại I

b) Xét ∆AIB và ∆AIC có:

AI là cạnh chung

AB = AC (do ∆ABC cân tại A)

IB = IC (cmt)

⇒ ∆AIB = ∆AIC (c-c-c)

⇒ ∠AIB = ∠AIC (hai góc tương ứng)

c) Do ∆AIB = ∆AIC (cmt)

⇒ ∠ABI = ∠ACI (hai góc tương ứng)

⇒ ∠FBI = ∠ECI

Xét ∆BIF và ∆CIE có:

∠FBI = ∠ECI (cmt)

IB = IC (cmt)

∠FIB = ∠EIC (đối đỉnh)

⇒ ∆BIF = ∆CIE (g-c-g)

⇒ IF = IE (hai cạnh tương ứng)

Hay IE = IF

d) ∆IBC cân tại I (cmt)

IH là đường trung trực của BC (cmt)

⇒ IH cũng là đường phân giác của ∆IBC

⇒ ∠BIH = ∠CIH

Ta có:

∠AIE = ∠BIH (đối đỉnh)

∠AIF = ∠CIH (đối đỉnh)

Mà ∠BIH = ∠CIH (cmt)

⇒ ∠AIE = ∠AIF

Xét ∆AIE và ∆AIF có:

IE = IF (cmt)

∠AIE = ∠AIF (cmt)

AI là cạnh chung

⇒ ∆AIE = ∆AIF (c-g-c)

⇒ AE = AF (hai cạnh tương ứng)

⇒ A nằm trên đường trung trực của EF (1)

Do IE = IF (cmt)

⇒ I nằm trên đường trung trực của EF (2)

Từ (1) và (2) ⇒ AI là đường trung trực của EF

⇒ AI ⊥ EF

⇒ AH ⊥ EF

Mà AH ⊥ BC (gt)

⇒ EF // BC

\(\left(x+2y\right)^3-x^2+4y^2\)

\(=\left(x+2y\right)^3-\left(x-2y\right)\left(x+2y\right)\)

\(=\left(x+2y\right)\left[\left(x+2y\right)^2-\left(x-2y\right)\right]\)

\(=\left(x+2y\right)\left(x^2+4xy+4y^2-x+2y\right)\)

a: Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH=\sqrt{4\cdot9}=6\left(cm\right)\)

Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

nên ADHE là hình chữ nhật

=>AH=DE

=>DE=6(cm)

b: ta có: ADHE là hình chữ nhật

=>\(\widehat{EAH}=\widehat{EDH}\)

mà \(\widehat{EAH}+\widehat{HCA}=90^0\)(ΔHAC vuông tại H)

và \(\widehat{EDH}+\widehat{MDH}=\widehat{MDE}=90^0\)

nên \(\widehat{MDH}=\widehat{HCA}\)

=>\(\widehat{MDH}=\widehat{MHD}\)

=>ΔMDH cân tại M

Ta có: \(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)

\(\widehat{MBD}+\widehat{MHD}=90^0\)(ΔHDB vuông tại D)

mà \(\widehat{MDH}=\widehat{MHD}\)

nên \(\widehat{MDB}=\widehat{MBD}\)

=>MB=MD

=>MB=MH

=>M là trung điểm của BH

c: Ta có: ADHE là hình chữ nhật

=>\(\widehat{HAD}=\widehat{HED}\)

mà \(\widehat{HAD}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)

và \(\widehat{HED}+\widehat{HEN}=\widehat{NED}=90^0\)

nên \(\widehat{HEN}=\widehat{HBA}\)

=>\(\widehat{NEH}=\widehat{NHE}\)

=>NE=NH

Ta có: \(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)

\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)

mà \(\widehat{NEH}=\widehat{NHE}\)

nên \(\widehat{NEC}=\widehat{NCE}\)

=>NE=NC

=>NH=NC

=>N là trung điểm của HC

Hanging out

hanging

Nghĩa gốc: 

- Hôm nay em tham gia thi chạy.

Nghĩa chuyển:

-Xe máy chạy nhanh hơn xe đạp.

- Nhà bác ý nghèo lắm, phải chạy ăn từng bữa.

-Đồng hồ chạy rất đúng giờ.

-Năm nay anh của em phải chạy nghĩa vụ quân sự.