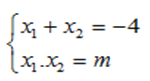Tìm giá trị nhỏ nhất của P=√1-x +√1+x +√4x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
19 tháng 12 2019
a) Khi m = -5 ta được phương trình x2 + 4x - 5 = 0
Ta có a + b + c = 1 + 4 + (-5) = 0 nên phương trình có hai nghiệm phân biệt là x1 = 1; x2= c/a = (-5)/1 = -5
Tập nghiệm của phương trình S = {1; -5}
b) Δ' = 22 - m = 4 - m
Phương trình có nghiệm kép ⇔ Δ'= 0 ⇔ 4 - m = 0 ⇔ m = 4
c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 
Ta có: x12 + x22 = 10 ⇔ (x1 + x2)2 - 2x1x2 = 10
⇔ (-4)2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
LC
0
19 tháng 12 2019
\(\frac{1}{a^2+b^2}+\frac{1}{2ab}\)
\(\ge\frac{4}{a^2+2ab+b^2}=\frac{4}{\left(a+b\right)^2}\)
19 tháng 12 2019
gọi I là giao điểm của SO với đường tròn.
theo tính chất hai tiếp tuyến cắt nhau ,ta có:
\(\widehat{AOS}=\widehat{SOD}\)\(=sđ\widebat{AI}=sđ\widebat{ID}\)
mà \(\widehat{ABD}=\frac{sđ\widebat{AD}}{2}=sđ\widebat{AI}\)
\(\Rightarrow\widehat{AOS}=\widehat{ABD}\)(đồng vị)
\(\Rightarrow SO//BD\)