1. What do you do?
2. Where does Mary meet her friends?
3. What do your parents do at the weekend?
4. When does your mum go shopping?
5. Who do you like cycling with?
6. Why are you into drawing pictures?

Bài 4B:

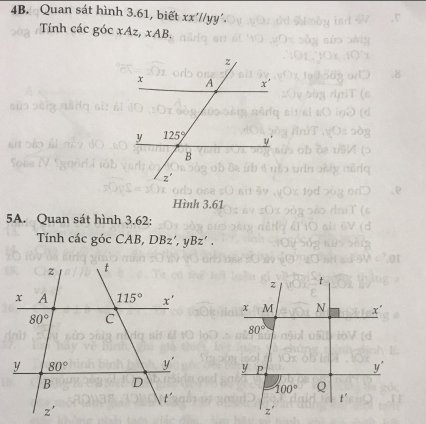
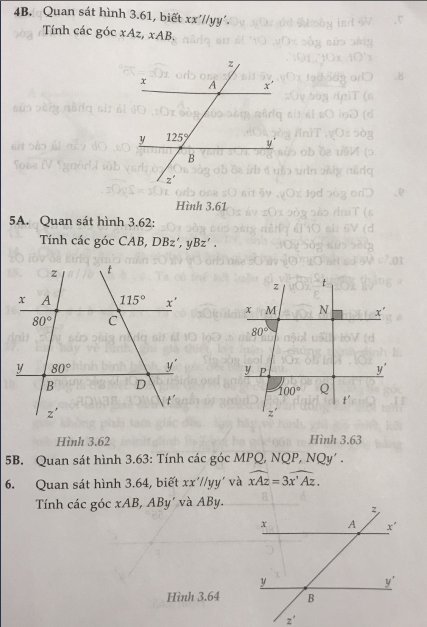
 \(\widehat{xAB}\) = 180⁰ - 125⁰ = 55⁰

\(\widehat{xAz}\) = \(\widehat{ABY}\) = 125⁰ (vì hai góc đồng vị)

5A. 

\(\widehat{CAB}\) = 180⁰ - 80⁰ = 100⁰

\(\widehat{CAB}\) = \(\widehat{DBZ'}\) = 100⁰ (hai góc đồng vị)

\(\widehat{YBZ'}\) = \(\widehat{ABD}\) = 80⁰

\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)

\(\Rightarrow x^3:\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)

\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^2\cdot\dfrac{1}{2}\)

\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^3\)

\(\Rightarrow x=\dfrac{1}{2}\)

\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\Rightarrow x^3=\dfrac{1}{2}.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}.\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^3\)

\(\Rightarrow x=\dfrac{1}{2}\)

\(18^3< 32^3< 32^9\)

\(\Rightarrow18^3< 32^9\Rightarrow\left(-18\right)^3>\left(-32\right)^9\)

Để so sánh hai số này, chúng ta có thể tính giá trị của mỗi số và so sánh kết quả.

Đầu tiên, tính giá trị của (-32)^9:

(-32)^9 = -134217728

Tiếp theo, tính giá trị của (-18)^3:

(-18)^3 = -5832

Kết quả là (-32)^9 = -134217728 lớn hơn (-18)^3 = -5832.

                          \(\dfrac{1}{7}\) = 0,(142875)

Mỗi chu kì tuần hoàn của số thập phân có số chữ số là: 6 chữ số. 

                         103 : 6 = 17 dư 1

Vậy chữ số thứ 103 sau dấu phẩy là chữ thứ 1 nhất của chu kỳ thứ:

                           17 + 1 = 18

Và đó là chữ số 1 

Chọn B. 1

may thế đúng phần mình ko  biết ;)

a, 7,2 +(-2,7) + 1,8 - 0,3

= (7,2 + 1,8) - (2,7 + 0,3)

=9 - 3

= 6

b, \(\dfrac{32}{5}\) + 11,5 - 6,7 + (2,4) - \(\dfrac{10}{4}\) + \(\dfrac{27}{10}\)

= 6,4 + 11,5 - 6,7 + 2,4 - 2,5 + 2,7

= (6,4 + 2,4) + ( 11,5 - 2,5) - (6,7 - 2,7)

= 8,8 + 9 - 4

= 8,8 + 5

= 13,8

tính nhanh nha

a) Do chỉ có 1 quả bóng màu vàng nên xác suất của biến cố A là \(\dfrac{1}{5}\)

b) Do không có quả bóng màu hồng nào nên xác suất của biến cố B là \(\dfrac{5}{5}=1\)

a) Vì trong bình có tổng cộng 5 quả bóng và chỉ có 1 quả màu vàng, nên khả năng thu được quả bóng màu vàng là 1.

Xác định kết quả của biến cố A là: P(A) = khả năng lấy được kết quả bóng màu vàng / tổng khả năng lấy bóng = 1/5 = 0,2

b) Vì trong bình không có quả bóng màu hồng nên không có khả năng thu được quả bóng màu hồng.

Xác định kết quả của biến cố B là: P(B) = khả năng lấy được kết quả bóng không có màu hồng / tổng khả năng lấy bóng = 0/5 = 0

a) Ta có: HA = 2RcosA HB = 2RcosB HC = 2RcosC AB = 2RsinC AC = 2RsinB Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2RsinC + 2RsinB Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < sinC + sinB Áp dụng bất đẳng thức tam giác, ta có: sinC + sinB > sin(A + B) = sinCOSA + cosCSINA = cosA + cosB Vậy ta có: cosA + cosB + cosC < sinC + sinB Do đó, ta có HA + HB + HC < AB + AC. b) Ta có: AB + BC + CA = 2R(sinA + sinB + sinC) = 2R(sinA + sinB + sin(A + B)) = 2R(2sin(A + B/2)cos(A - B/2) + sin(A + B)) = 4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B) Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2332​ (4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B)) Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < 1166​(2sin(A + B/2)cos(A - B/2) + sin(A + B)) Áp dụng bất đẳng thức tam giác, ta có: sin(A + B) > sinC = sin(A + B/2 + B/2) = sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) Vậy ta có: 2sin(A + B/2)cos(A - B/2) + sin(A + B) < 2sin(A + B/2)cos(A - B/2) + sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + sin(B/2)cos(A + B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2)) Vậy ta có: cosA + cosB + cosC < 1166​(2sin(A + B/2)cos(A - B/2) + sin(A + B)) < 1166​(sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2))) Do đó, ta có HA + HB + HC < 2332​(AB + BC + CA).

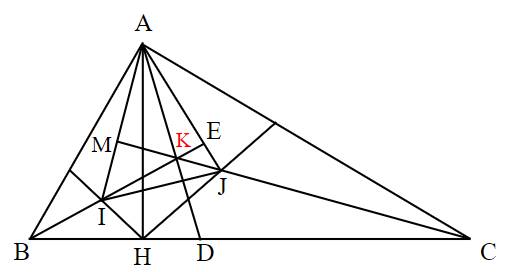
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC

^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.

Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.

=> Tam giác ABE vuông tại E (đpcm)

b) Gọi M là giao điểm của CJ và AI.

Gọi K là giao điểm của BE và CM.

^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM

^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.

Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.

=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.

Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.

BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.

=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)