Version:0.9 StartHTML:0000000105 EndHTML:0000001679 StartFragment:0000000141 EndFragment:0000001639
Một hộp quà có dạng hình chóp tam giác đều có cạnh bên là 35 cm và độ dài trung đoạn là 15 cm với khung bằng nhựa, đáy và các mặt xung quanh bọc vải. a) Tính thể tích của hộp quà b) Hỏi diện tích vải dùng để làmchiếc hộp đó là bao nhiêu? (coi phần các mép vải khâu nối không đáng kể)Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{11}{19}.\dfrac{12}{29}-\dfrac{11}{19}.\dfrac{2}{29}+\dfrac{11}{19}.\dfrac{19}{29}\)
\(=\dfrac{11}{19}.\left(\dfrac{12}{29}-\dfrac{2}{29}+\dfrac{19}{29}\right)\)
\(=\dfrac{11}{19}.1\)
\(=\dfrac{11}{19}\)

a: 15p=0,25 giờ
Vận tốc trung bình mà Lan đi xe đạp từ nhà đến trường là:
1,8:0,25=7,2(km/h)
b: Thời gian còn lại là 15-1,5=13,5(phút)=0,225(giờ)
vận tốc Lan cần phải đi là:
1,8:0,225=8(km/h)

\(C=3+2\sqrt{4x^2-8x+13}\)
\(=3+2\sqrt{4x^2-8x+4+9}\)
\(=3+2\sqrt{\left(2x-2\right)^2+9}>=3+2\cdot\sqrt{9}=9\)
Dấu '=' xảy ra khi 2x-2=0
=>x=1
\(D=\left(\sqrt{x}-6\right)^2+\left(\sqrt{x}+2\right)^2\)
\(=x-12\sqrt{x}+36+x+4\sqrt{x}+4\)
\(=2x-8\sqrt{x}+40\)
\(=2\left(x-4\sqrt{x}+20\right)\)
\(=2\left(x-4\sqrt{x}+4+16\right)\)
\(=2\left(\sqrt{x}-2\right)^2+32>=32\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}-2=0\)
=>x=4
\(F=x+y-2\sqrt{x+2}-4\sqrt{y-1}+10\)
\(=x+2-2\sqrt{x+2}+1+y-1-4\sqrt{y-1}+4+4\)
\(=\left(\sqrt{x+2}-1\right)^2+\left(\sqrt{y-1}-2\right)^2+4>=4\forall x,y\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x+2=1\\y-1=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=5\end{matrix}\right.\)

\(B=6x^4+5x^2y^2+y^4+6x^2-2\)
\(=6x^4+2x^2y^2+3x^2y^2+y^4+6x^2-2\)
\(=2x^2\left(3x^2+y^2\right)+y^2\left(3x^2+y^2\right)+6x^2-2\)
\(=12x^2+18y^2+6x^2-2\)
\(=18x^2+18y^2-2=18x^2+6y^2+12y^2-2\)
\(=6\left(3x^2+y^2\right)+12y^2-2=36+12y^2-2=12y^2+34\)

a: Xét ΔAHN vuông tại N và ΔACH vuông tại H có
\(\widehat{HAN}\) chung
Do đó: ΔAHN~ΔACH
b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB\)
=>\(AM\cdot15=12^2=144\)
=>AM=9,6(cm)
c: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AN\cdot AC\)
=>\(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{15^2-12^2}=9\left(cm\right)\)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(HC=\sqrt{13^2-12^2}=5\left(cm\right)\)
BC=BH+CH=9+5=14(cm)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN~ΔACB
=>\(\dfrac{MN}{CB}=\dfrac{AM}{AC}\)
=>\(\dfrac{MN}{14}=\dfrac{9.6}{13}\)
=>\(MN=\dfrac{672}{65}\left(cm\right)\)

Nửa chu vi nhà Lan là 86:2=43(m)
Chiều dài là (43+7):2=25(m)
Chiều rộng là 25-7=18(m)
Diện tích là 25x18=450(m2)
Diện tích phần đất làm vườn là:
\(450\times\left(1-\dfrac{2}{5}\right)=450\times\dfrac{3}{5}=270\left(m^2\right)\)

câu a)
thể tích hội trường :
\(8.5\cdot7\cdot4=238\left(m^3\right)\)
80% của hội trường :
\(238\cdot\dfrac{80}{100}=190.4\left(m^3\right)\)
Số người tại Hội trường :
\(190.4\cdot5.6=34\left(người\right)\)

(d')//(d)
=>\(\left\{{}\begin{matrix}a=-1\\b\ne-2\end{matrix}\right.\)
vậy: (d'): y=-x+b
Thay x=-1 và y=3 vào (d'), ta được:
b+1=3
=>b=2(nhận)
vậy: y=-x+2
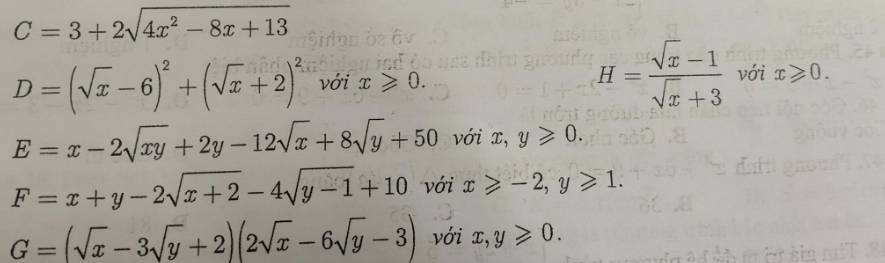

Ý a phải là tính diện tích của hộp quà chứ bạn đề bài làm gì cho chiều cao của hình chóp tam giác đâu mà tính thể tích