Nếu tung một đồng xử 15 lần liên tiếp, có 7 lần xuất hiện mặt N(mặt ngữa) thì xác suất thực nghiệm xuất hiện mặt N(mặt ngữa) bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số lần xuất hiện mặt 4 chấm là:
2 . 2 = 4 (lần)
Xác suất thực nghiệm của sự kiện xuất hiện mặt 4 chấm là:
4/20 = 1/5 = 20%
Chọn D

a: Trên tia Ox, ta có: OB<OA
nên B nằm giữa O và A
=>OB+BA=OA
=>BA+3=7
=>BA=4(cm)
b: Trên tia Ox, ta có: OC<OA
nên C nằm giữa O và A
=>OC+CA=OA
=>CA+5=7
=>CA=2(cm)
Trên tia Ox, ta có: OB<OC
nên B nằm giữa O và C
=>OB+BC=OC
=>BC+3=5
=>BC=2(cm)
Vì BC+CA=BA
nên C nằm giữa B và A
c: Ta có: C nằm giữa B và A
CB=CA(=2cm)
Do đó: C là trung điểm của AB

\(A=\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{3843}\)
\(=\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{61\cdot63}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{61\cdot63}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{61}-\dfrac{1}{63}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{63}\right)=\dfrac{1}{2}\cdot\dfrac{20}{63}=\dfrac{10}{63}\)

Yêu cầu đề bài là gì vậy bạn? Và bạn xem lại xem biểu thức đã viết đúng chưa nhé.

Bài 6:
Tỉ số phần trăm giữa khối lượng táo khô và táo tươi là:
100%-75%=25%
Khối lượng táo tươi cần tới là:
300:25%=1200(g)

M thuộc đoạn $AB$, mà $AM=AB$? Bạn xem lại đề nhé. Như thế này thì $M$ trùng $B$ rồi.

1: \(\left(\dfrac{3}{4}\right)^2\cdot4^2-\left(\dfrac{1}{2}\right)^2:2-2\dfrac{3}{4}\)
\(=\left(\dfrac{3}{4}\cdot4\right)^2-\dfrac{1}{8}-\dfrac{11}{4}\)
\(=9-\dfrac{1}{8}-\dfrac{22}{8}=9-\dfrac{23}{8}=\dfrac{72-23}{8}=\dfrac{49}{8}\)
2: \(\left(\dfrac{3}{5}\right)^2\cdot5^2-\left(2\dfrac{1}{4}\right)^3:\left(\dfrac{3}{4}\right)^3-3\)
\(=\left(\dfrac{3}{5}\cdot5\right)^2-\left(\dfrac{9}{4}:\dfrac{3}{4}\right)^3-3\)
\(=3^2-3^3-3=9-27-3=9-30=-21\)
3: \(25\cdot\left(-\dfrac{1}{5}\right)^3+\dfrac{1}{5}-2\cdot\left(-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\)
\(=25\cdot\dfrac{-1}{125}+\dfrac{1}{5}-2\cdot\dfrac{1}{4}-\dfrac{1}{2}\)
\(=-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{2}-\dfrac{1}{2}=-1\)
4: \(4\cdot\left(\dfrac{1}{2}\right)^3+3\cdot\left(\dfrac{1}{2}\right)^2-2\cdot\left(\dfrac{1}{2}\right)^0\)
\(=4\cdot\dfrac{1}{8}+3\cdot\dfrac{1}{4}-2\)
\(=\dfrac{1}{2}+\dfrac{3}{4}-2=\dfrac{5}{4}-2=-\dfrac{3}{4}\)
5: \(\left(-\dfrac{1}{2}\right)^2\cdot4+\dfrac{1}{3}\cdot3^2+\left(\dfrac{1}{2020}\right)^0\)
\(=\dfrac{1}{4}\cdot4+\dfrac{1}{3}\cdot9+1\)
=1+3+1
=5
6: \(5\cdot\left(-\dfrac{2}{5}\right)^2+2\cdot\dfrac{-2}{5}+4\cdot\left(-\dfrac{2}{5}\right)^0\)
\(=5\cdot\dfrac{4}{25}-\dfrac{4}{5}+4\)
\(=\dfrac{4}{5}-\dfrac{4}{5}+4=4\)


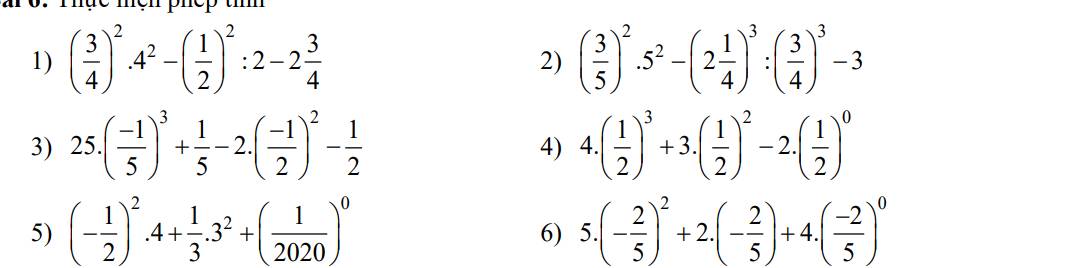
Giải
Xác suất thực nghiệm xuất hiện mặt ngửa là:
7 : 15 = \(\dfrac{7}{15}\)
Kết luận:Xác xuất thực nghiệm xuất hiện mặt ngửa là \(\dfrac{7}{15}\)