Chứng minh rằng: n(n+1).( 2n+1) chia hết cho 6 với n thuộc N
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{xy^2}{xy+y}=\dfrac{xy^2}{y\left(x+1\right)}=\dfrac{xy}{x+1}\\ b,\dfrac{xy-y}{x}\ne\dfrac{xy-x}{y}\\ c,\dfrac{3ac}{a^3b}=\dfrac{3c}{a^2b}=\dfrac{6c}{2a^2b}\\ d,\dfrac{3ab-3b^2}{6b^2}=\dfrac{3b\left(a-b\right)}{6b^2}=\dfrac{a-b}{2b}\\ e,\dfrac{3x\left(x-y\right)^2}{9x^2\left(x-y\right)}=\dfrac{3x\left(x-y\right)}{9x^2}=\dfrac{x-y}{3x}\\ f,\dfrac{8-x^3}{x\left(x^2+2x+4\right)}=\dfrac{-\left(x^3-8\right)}{x\left(x^2+2x+4\right)}=\dfrac{-\left(x-2\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}=\dfrac{-\left(x-2\right)}{x}=\dfrac{x-2}{-x}\)

ĐK: `x>=0`
Ta có:
\(B=\dfrac{5\sqrt{x}-1}{\sqrt{x}+1}\\ =\dfrac{\left(5\sqrt{x}+5\right)-6}{\sqrt{x}+1}=\dfrac{5\left(\sqrt{x}+1\right)-6}{\sqrt{x}+1}\\ =\dfrac{5\left(\sqrt{x}+1\right)}{\sqrt{x}+1}-\dfrac{6}{\sqrt{x}+1}\\ =5-\dfrac{6}{\sqrt{x}+1}\)
Vì: \(\sqrt{x}\ge0\forall x\)
\(=>\sqrt{x}+1\ge1\forall x=>\dfrac{6}{\sqrt{x}+1}\le6\\ =>5-\dfrac{6}{\sqrt{x}+1}\ge5-6=-1\)
Dấu "=" xảy ra: `x=0`

Ta có pt hoành độ giao điểm là:
\(-x^2=\left(2-m\right)x+m-3\\ \Leftrightarrow x^2+\left(2-m\right)x+m-3=0\)
Để pt có nghiệm phân biệt thì:
\(\Delta=\left(2-m\right)^2-4\cdot1\cdot\left(m-3\right)\\ =4-4m+m^2-4m+12=m^2-8m+16=\left(m-4\right)^2>0\)
`=>m-4<>0<=>m<>4`
Ta có: `a+b+c=1+(2-m)+(m-3)=0`
\(=>x_1=1\)
Theo vi-ét ta có: \(x_1+x_2=m-2=>x_2=m-2-x_2=m-2-1=m-3\)
\(\left|x_1\right|+x_2^2=2\\ =>1+\left(m-3\right)^2=2\\< =>\left(m-3\right)^2=2-1=1\\ < =>\left[{}\begin{matrix}m-3=1\\m-3=-1\end{matrix}\right.\\ < =>\left[{}\begin{matrix}m=1+3=4\left(ktm\right)\\m=-1+3=2\left(tm\right)\end{matrix}\right.\)
Vậy: ...

Bài 22:
\(a^6+b^6\\ =\left(a^2\right)^3+\left(b^2\right)^3\\ =\left(a^2+b^2\right)\left[\left(a^2\right)^2-a^2b^2+\left(b^2\right)^2\right]\\ =\left(a^2+b^2\right)\left[\left(a^4+2a^2b^2+b^4\right)-3a^2b^2\right]\\ =\left(a^2+b^2\right)\left[\left(a^2+b^2\right)^2-3a^2b^2\right]\)
Bài 24:
a) Ta có:
`(a+b)^2=2(a^2+b^2)`
`<=>a^2+2ab+b^2=2a^2+2b^2`
`<=>a^2-2ab+b^2=0`
`<=>(a-b)^2=0`
`<=>a-b=0`
`<=>a=b`
b) Ta có:
`a^2+b^2+c^2=ab+bc+ca`
`<=>2a^2+2b^2+2c^2=2ab+2bc+2ca`
`<=>(a^2-2ab+b^2)+(a^2-2ca+c^2)+(b^2-2bc+c^2)=0`
`<=>(a-b)^2+(a-c)^2+(b-c)^2=0`
`<=>a-b=0` và `a-c=0` và `b-c=0`
`<=>a=b=c`
c) Ta có:
`(a+b+c)^2=3(ab+bc+bc)`
`<=>a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca`
`<=>a^2+b^2+c^2=ab+bc+ca`
`<=>(a-b)^2+(b-c)^2+(a-c)^2=0`
`<=>a=b=c`

ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{15^2-9^2}=12\left(cm\right)\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=24\left(cm\right)\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{15^2+15^2-24^2}{2\cdot15\cdot15}=\dfrac{-7}{25}\)
=>\(sinBAC=\sqrt{1-\left(-\dfrac{7}{25}\right)^2}=\sqrt{1-\dfrac{49}{625}}=\dfrac{24}{25}\)
Xét ΔABC có \(\dfrac{BC}{sinBAC}=2R\)
=>\(2R=24:\dfrac{24}{25}=25\)
=>R=12,5(cm)

\(\left[19\left(4\cdot2^3+18\right)-9\cdot50\right]:5^2\\ =\left[19\left(4\cdot8+18\right)-450\right]:25\\ =\left[19\cdot50-450\right]:25\\ =\left[950-450\right]:25\\ =500:25\\ =20\)
\(\left[19\left(4\cdot2^3+18\right)-9\cdot50\right]:5^2\\ =\left[19\left(4\cdot8+18\right)-9\cdot50\right]:25\\ =\left[19\left(32+18\right)-9\cdot50\right]:25\\ =\left(19\cdot50-9\cdot50\right):25\\ =50\cdot\left(19-9\right):25\\ =\left(50:25\right)\cdot10\\ =2\cdot10\\ =20\)


Đây là toán nâng cao chuyên đề toán hai hiệu số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Hiệu số học sinh mỗi tổ trong hai cách chia là:
10 - 9 = 1 (học sinh)
Hiệu số học sinh trong hai cách chia là:
3 + 1 = 4 (học sinh)
Số tổ là: 4 : 1 = 4 (tổ)
Số học sinh lớp 5A là: 9 x 4 + 1 = 37 (học sinh)
Đáp số:

Bài 2:
\(1)25-12\cdot2+2^3\\ =25-24+2^3\\ =1+8\\ =9\\ 2)45-12\cdot3+2^3\\ =45-36+2^3\\ =9+8\\ =17\\ 3)32+5\cdot13-3\cdot2^3\\ =32+65-3\cdot8\\ =97-24\\ =73\\ 4)150+50:5-2\cdot3^2\\ =150+10-2\cdot9\\ =160-18\\ =142\\ 5)35-2\cdot1^{111}+3\cdot7^2\\ =35-2\cdot1+3\cdot49\\ =35-2+147\\ =33+147\\ =180\\ 6)2023-5^3:25+27\\ =2023-125:25+27\\ =2023-5+27\\ =2023+22\\ =2045\)
Bài 1:
1: \(3^2\cdot5^3+9^2=9\cdot125+81=1206\)
2: \(55+45:3^2=55+45:9=55+5=60\)
3: \(8^3:4^2-5^2=\dfrac{2^6}{2^4}-25=2^2-25=4-25=-21\)
4: \(5\cdot3^2-32:2^2=5\cdot9-2^3=45-8=37\)
5: \(16:2^3+5^2\cdot4=16:8+25\cdot4=2+100=102\)
6: \(5\cdot2^2-18:3^2=5\cdot4-18:9=20-2=18\)
7: \(3\cdot5^2-15\cdot2^2=3\cdot25-15\cdot4=75-60=15\)
8: \(2^3\cdot6-72:3^2=8\cdot6-72:9=48-8=40\)
9: \(5\cdot2^2-27:3^2=5\cdot4-27:9=20-3=17\)
10: \(3\cdot2^4+81:3^2=3\cdot16+81:9=48+9=57\)
11: \(4\cdot5^3-32:2^5=4\cdot125-32:32=500-1=499\)
12: \(6\cdot5^2-32:2^4\)
\(=6\cdot25-32:16\)
=150-2=148
Bài 3:
1: \(2^8:2^4+3^2\cdot3\)
\(=2^4+3^3\)
=16+27=43
2: \(3^{24}:3^{21}+2^2\cdot2^3\)
\(=3^3+2^5\)
=27+32=59
3: \(5^9:5^7+12\cdot3+7^0\)
\(=5^2+4+1\)
=25+5=30
4: \(5^6:5^4+3^2-2021^0\)
\(=5^2+9-1\)
=25+8=33
5: \(3^{19}:3^{16}+5^2\cdot2^3-1^{2021}\)
\(=3^3+25\cdot8-1\)
=200+26=226
6: \(3^6:3^5+2\cdot2^3+2021^0\)
\(=3+2^4+1\)
=4+16=20

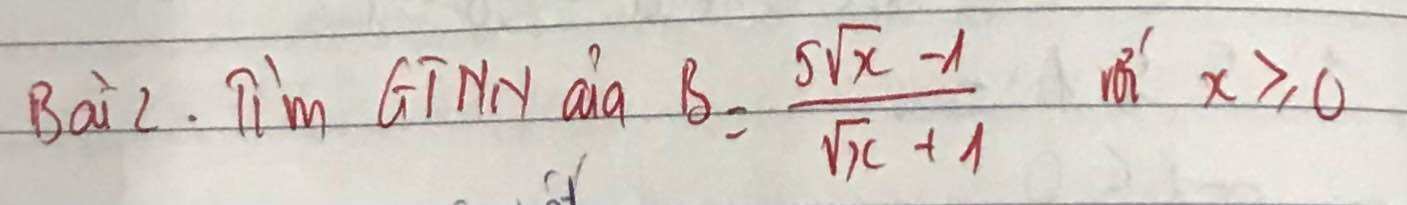
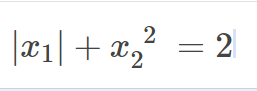

\(n\left(n+1\right)\left(2n+1\right)\\ =n\left(n+1\right)\left[2n-2+3\right]\\ =n\left(n+1\right)\left(2n-2\right)+3n\left(n+1\right)\\ =2\left(n-1\right)n\left(n+1\right)+3n\left(n+1\right)\)
Ta có:
`+)(n-1)n(n+1)` là tích của 3 số tự nhiên liên tiếp `=>(n-1)n(n+1)` chia hết cho 3
`=>2(n-1)n(n+1)` chia hết cho 6 (1)
`+)n(n+1)` là tích của 2 số tự nhiên liên tiếp `=>n(n+1)` chia hết cho 2
`=>3n(n+1)` chia hết cho 6 (2)
Từ (1) và (2) => `n(n+1)(2n+1)` chia hết cho 6