cho Ox và Oy là hai tia đối nhau. Trên tia Ox lấy điểm A sao cho OA=2cm. Trên tia Oy lấy 2 điểm B và C ( B nằm giữa O và C ) sao cho OB=1cm ; OC = 7cm. Gọi D là trung điểm của BC
Tính BC ; AB
B có là trug điểm của AD không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc xe máy là x(km/h)
(ĐK: x>0)
Vận tốc xe ô tô là x+20(km/h)
CB=AB-AC=80km
Thời gian ô tô đi từ B đến chỗ gặp là \(\dfrac{80}{x+20}\left(giờ\right)\)
Thời gian xe máy đi từ A đến chỗ gặp là \(\dfrac{120}{x}\left(giờ\right)\)
Do đó, ta có phương trình:
\(\dfrac{80}{x+20}=\dfrac{120}{x}\)
=>\(\dfrac{2}{x+20}=\dfrac{3}{x}\)
=>3(x+20)=2x
=>3x+60=2x
=>x=-60
=>Đề sai rồi bạn

0,5 . [ ( -4,9) - 3,1 ] - 0,15 : 0,1
0,5 . ( -8 ) - 1,5
4-1,5 = 2,5
\(0,5\cdot\left(-4,9\right)-0,5\cdot3,1-0,15:0,1\)
\(=0,5\cdot\left(-4.9-3,1\right)-0,15\cdot10\)
\(=-0,5\cdot8-1,5=-4-1,5=-5,5\)

\(0,5\cdot\left(-4,9\right)-0,5\cdot3,1\cdot\left(-0,15\right):0,1\)
\(=0,5\cdot\left(-4,9\right)+0,5\cdot3,1\cdot0,15\cdot10\)
\(=0,5\cdot\left(-4,9\right)+0,5\cdot3,1\cdot1,5\)
\(=0,5\left(-4,9+3,1\cdot1,5\right)=0,5\cdot\left(-0,25\right)=-0,125\)
0,5⋅(−4,9)−0,5⋅3,1⋅(−0,15):0,1
=0,5⋅(−4,9)+0,5⋅3,1⋅0,15⋅10=0,5⋅(−4,9)+0,5⋅3,1⋅0,15⋅10
=0,5⋅(−4,9)+0,5⋅3,1⋅1,5=0,5⋅(−4,9)+0,5⋅3,1⋅1,5
=0,5(−4,9+3,1⋅1,5)=0,5⋅(−0,25)=−0,125=0,5(−4,9+3,1⋅1,5)=0,5⋅(−0,25)=−0,125
ko biết đúng ko thôi

a) Chiều rộng thửa ruộng:
60 × 2/3 = 40 (m)
Diện tích thửa ruộng:
60 × 40 = 2400 (m²)
b) Số kg thóc thu được từ thửa ruộng:
2400 × 2/3 = 1600 (kg)
a: Chiều rộng thửa ruộng là \(60\times\dfrac{2}{3}=40\left(m\right)\)
Diện tích thửa ruộng là 60x40=2400(m2)
b: Khối lượng thóc thu hoạch được là:
\(2400\times\dfrac{2}{3}=1600\left(kg\right)\)

2x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{2};\dfrac{x}{y}=\dfrac{3}{2};\dfrac{3}{x}=\dfrac{2}{y};\dfrac{y}{x}=\dfrac{2}{3}\)

a: Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Sửa đề: A là trung điểm của BD, DK cắt CA tại N
Xét ΔCDB có
CA,DK là các đường trung tuyến
CA cắt DK tại M
Do đó: M là trọng tâm của ΔCDB
=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot12=8\left(cm\right)\)
c: Sửa đề; Chứng minh B,M,Q thẳng hàng
Gọi I là trung điểm của CA
Đường trung trực của AC cắt CD tại Q
mà I là trung điểm của AC
nên QI\(\perp\)AC và I là trung điểm của aC
=>QI//DA
Xét ΔCAD có
I là trung điểm của CA
IQ//DA
Do đó: Q là trung điểm của CD
Xét ΔCDB có
M là trọng tâm
Q là trung điểm của CD
Do đó: B,M,Q thẳng hàng

a: ΔABC vuông tại B
=>\(AB^2+BC^2=AC^2\)
=>\(AC=\sqrt{12^2+9^2}=15\left(cm\right)\)
b: Xét ΔHBA vuông tại H và ΔHCB vuông tại H có
\(\widehat{HBA}=\widehat{HCB}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA~ΔHCB
=>\(\dfrac{HB}{HC}=\dfrac{HA}{HB}\)
=>\(HB^2=HA\cdot HC\)
c: Đề sai rồi bạn
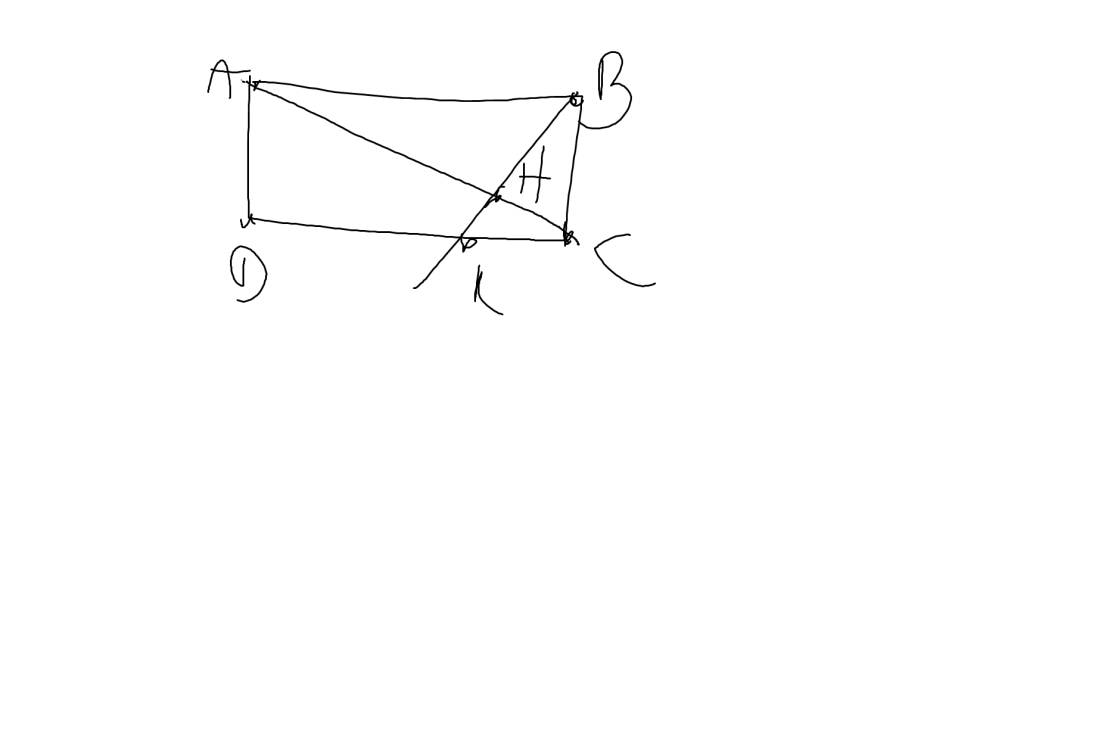

1: Xét ΔABC có
BN,CM là các đường trung tuyến
BN cắt CM tại D
Do đó: D là trọng tâm của ΔABC
=>\(BD=\dfrac{2}{3}BN;CD=\dfrac{2}{3}CM\)
BD=2/3BN
=>\(S_{ABD}=\dfrac{2}{3}\cdot S_{ABN}\left(1\right)\)
\(CD=\dfrac{2}{3}CM\)
=>\(S_{ADC}=\dfrac{2}{3}\cdot S_{AMC}\left(2\right)\)
Ta có: M là trung điểm của AB
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}\left(3\right)\)
Ta có: N là trung điểm của AC
=>\(S_{ABN}=\dfrac{1}{2}\cdot S_{ABC}\left(4\right)\)
Từ (1),(2),(3),(4) suy ra \(S_{ABN}=S_{ADC}\)
mà \(S_{MBN}=\dfrac{1}{2}\cdot S_{ANB}\)
và \(S_{MNC}=\dfrac{1}{2}\cdot S_{AMC}\)
nên \(S_{MBN}=S_{MNC}\)
=>\(S_{MBD}+S_{MDN}=S_{NDC}+S_{MDN}\)
=>\(S_{MBD}=S_{NDC}\)
2: \(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot30=15\left(cm^2\right)\)
=>\(S_{MNC}=\dfrac{1}{2}\cdot S_{AMC}=7,5\left(cm^2\right)\)
Vì CD=2/3CM
nên \(S_{CND}=\dfrac{2}{3}\cdot S_{CNM}=5\left(cm^2\right)\)

\(AN=\dfrac{2}{3}AC\)
=>AC=1,5AN
=>\(S_{AMC}=1,5\times S_{AMN}=1,5\times20=30\left(cm^2\right)\)
BM=1/3BC
=>\(CM=\dfrac{2}{3}CB\)
=>CB=1,5CM
=>\(S_{ABC}=1,5\times S_{AMC}=1,5\times30=45\left(cm^2\right)\)
a: Trên tia Oy, ta có: OB<OC
nên B nằm giữa O và C
=>OB+BC=OC
=>BC+1=7
=>BC=6(cm)
Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>AB=OA+OB=2+1=3(cm)
b: D là trung điểm của BC
=>\(BD=\dfrac{BC}{2}=3\left(cm\right)\)
Vì BD=BA(=3cm)
nên B là trung điểm của AD