có a+2b=a+b+b<=>a+a+b

hay a+2b=2a+b

=> a+2b chia hết cho 3 <=>2a+b chia hết cho 3

Ta có a + 2b \(⋮\)3

<=> \(3a+3b-2a-b⋮3\)

<=> 3(a + b) - (2a + b) \(⋮\)3

Vì 3(a + b) \(⋮\)3

<=> 2a + b \(⋮\)3

Tứ giác ADCD có góc B =  góc A+10 , góc C = góc B + 10 , góc D = góc C + 10 .Khẳng định nào sao đây là đúng :

A  . góc  A bằng  65  độ 

B  . góc  B  bằng 85 độ 

C  . góc C  bằng  100 độ 

D  . góc  D bằng   90 độ 

góc C= B+10 tức là góc C= góc A +20  tương tự góc D = C +10 thì tức là góc D=góc A +30

có tứ giác ABCD có GÓC A+ GÓC B+ GÓC C + GÓC D = 360 ĐỘ= A+(A+10)+(A+20)+(A+30)=4A +60

4A=360 -60=300 ĐỘ

GÓC A=3OO/A=75 ĐỘ

GÓC B=75 +10=85 ĐỘ

GÓC C =75 +20=95 ĐỘ 

GÓC D=75 +30=105 ĐỘ

VẬY NÊN ĐÁP ÁN B ĐÚNG

Trong \(3\)số \(a,b,c\)chắc chắn có ít nhất hai số cùng tính chẵn lẻ, không mất tính tổng quát, giả sử đó là \(a,b\).

Khi đó \(a+b⋮2\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)⋮2\).

\(\left(a^3+b^3+c^3\right)⋮6\Leftrightarrow\left[a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\right]⋮6\)

\(\Leftrightarrow\left(a+b+c\right)^3⋮6\Leftrightarrow\left(a+b+c\right)⋮6\).

Trả lời:

25x² + 20x + 4 

= ( 5x )² + 2 . 5x . 2 + 2² 

= ( 5x + 2 )²

Trả lời: 

25x + 20x + 4

= ( 5x ) ²   + 2.5x.2 + 2 ²

= ( 5x + 2 ) ²

A B C D

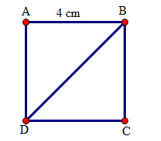
Gọi hình vuông ABCD có cạnh là 4 cm với đường chéo AD

có tam giác ACD vuông tại C

=> AC²+CD²=AD² ( định lí Pitago)

4² .2=AD²

32=AD²

AD²=\(\sqrt{32}\)

Xét tam giác ABD vuông tại A, ta có:

BD² = AB² + AD² 

BD² = 4² + 4²

BD² = 16 + 16

BD² = 32

BD = \(\sqrt{32}\)\(=4\sqrt{2}\left(cm\right)\)

\(\left(x^2+6\right)\left(2x-5\right)\ge0\)

\(\Rightarrow2x-5\ge0\)vì \(x^2+6\ge0\forall x\)

\(\Leftrightarrow-5\ge-2x\Leftrightarrow x\ge\frac{5}{2}\)

Vậy tập nghiệm BFT là S = { x | x >= 5/2 } 

Ta thấy (x²+6)(2x-5)>=0 mà x²+6 > 0 => 2x-5>=0 <=> x >=5/2

Ta có x - y = 4

=> y = x - 4

Khi đó Q = x² + 8y + 10 = x² + 8(x - 4) + 10 

= x² + 8x - 22 = x² + 8x + 16 - 38 = (x + 4)² - 38 \(\ge-38\)

Dấu "=" xảy ra <=> x + 4 = 0 <=> x =-4

=> y = -8

Vậy Min Q = -38 <=> x = -4 ; y = -8

đáp án C

Trả lời :

C. (tui đoán)

~HT~