Cho góc nhọn xOy. Vẽ đường thẳng a vuông góc với Ox,đường thẳng b vuông góc với Oy.Chứng tỏ rằng a cắt b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$(2x-15)^3=(2^2.3^3-2^3.3^2):(-36)=2^2.3^2(3-2):(-36)=36:(-36)=-1$
$\Rightarrow 2x-15=-1$ hoặc $2x-15=1$
$\Rightarrow x=7$ hoặc $x=8$
Bạn lưu ý lần sau gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

Bài nào em chưa biết cách làm thì hỏi để Thầy cô và các bạn hướng dẫn. Em không gửi một tệp bài lên nhờ mọi người giải như vậy em sẽ không học tập phát triển được.

Bài 1:
a: \(\dfrac{-3}{5}+\dfrac{7}{21}+\dfrac{-4}{5}+\dfrac{7}{5}\)
\(=\left(-\dfrac{3}{5}-\dfrac{4}{5}+\dfrac{7}{5}\right)+\dfrac{7}{21}\)
\(=\dfrac{7}{21}=\dfrac{1}{3}\)
b: \(-\dfrac{3}{17}+\left(\dfrac{2}{3}+\dfrac{3}{17}\right)\)
\(=-\dfrac{3}{17}+\dfrac{3}{17}+\dfrac{2}{3}\)
\(=0+\dfrac{2}{3}=\dfrac{2}{3}\)
c: \(\dfrac{-5}{21}+\left(\dfrac{-16}{21}+1\right)\)
\(=\left(-\dfrac{5}{21}-\dfrac{16}{21}\right)+1\)
=-1+1=0
d: \(\dfrac{5}{7}+\dfrac{9}{23}+\dfrac{-12}{7}+\dfrac{14}{23}\)
\(=\left(\dfrac{5}{7}-\dfrac{12}{7}\right)+\left(\dfrac{9}{23}+\dfrac{14}{23}\right)\)
\(=-1+1=0\)
e: \(\dfrac{3}{17}+\dfrac{-5}{13}+\dfrac{-18}{35}+\dfrac{14}{17}+\dfrac{17}{-35}+\dfrac{-8}{13}\)
\(=\left(\dfrac{3}{17}+\dfrac{14}{17}\right)+\left(-\dfrac{5}{13}-\dfrac{8}{13}\right)+\left(-\dfrac{18}{35}-\dfrac{17}{35}\right)\)
=1-1-1
=-1
f: \(\dfrac{-3}{8}\cdot\dfrac{1}{6}+\dfrac{3}{-8}\cdot\dfrac{5}{6}+\dfrac{-10}{16}\)
\(=\dfrac{-3}{8}\left(\dfrac{1}{6}+\dfrac{5}{6}\right)+\dfrac{-5}{8}\)
\(=-\dfrac{3}{8}-\dfrac{5}{8}=-1\)
g: \(\dfrac{-4}{11}\cdot\dfrac{5}{15}\cdot\dfrac{11}{-4}=\dfrac{-4}{-4}\cdot\dfrac{11}{11}\cdot\dfrac{1}{3}=\dfrac{1}{3}\)
h: \(\dfrac{7}{36}-\dfrac{8}{-9}+\dfrac{-2}{3}\)
\(=\dfrac{7}{36}+\dfrac{8}{9}-\dfrac{2}{3}\)
\(=\dfrac{7}{36}+\dfrac{32}{36}-\dfrac{24}{36}=\dfrac{15}{36}=\dfrac{5}{12}\)
i: \(\dfrac{4}{7}+\dfrac{-5}{8}-\dfrac{3}{28}\)
\(=\dfrac{32}{56}-\dfrac{35}{56}-\dfrac{6}{56}\)
\(=-\dfrac{9}{56}\)
l: \(\dfrac{-6}{11}:\left(\dfrac{3}{5}\cdot\dfrac{4}{11}\right)\)
\(=-\dfrac{6}{11}:\dfrac{12}{55}\)
\(=-\dfrac{6}{11}\cdot\dfrac{55}{12}=\dfrac{-5}{2}\)

Dạng 2:
a: \(1\dfrac{3}{4}x-5=3\dfrac{1}{3}\)
=>\(x\cdot\dfrac{7}{4}-5=\dfrac{10}{3}\)
=>\(x\cdot\dfrac{7}{4}=\dfrac{10}{3}+5=\dfrac{25}{3}\)
=>\(x=\dfrac{25}{3}:\dfrac{7}{4}=\dfrac{25}{3}\cdot\dfrac{4}{7}=\dfrac{100}{21}\)
b: \(\dfrac{2}{3}x+\dfrac{1}{4}=\dfrac{7}{12}\)
=>\(\dfrac{2}{3}x=\dfrac{7}{12}-\dfrac{1}{4}=\dfrac{7}{12}-\dfrac{3}{12}=\dfrac{4}{12}=\dfrac{1}{3}\)
=>\(x=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\)
c: \(\dfrac{1}{3}+\dfrac{2}{5}\left(x+1\right)=1\)
=>\(\dfrac{2}{5}\left(x+1\right)=1-\dfrac{1}{3}=\dfrac{2}{3}\)
=>\(x+1=\dfrac{2}{3}:\dfrac{2}{5}=\dfrac{5}{3}\)
=>\(x=\dfrac{5}{3}-1=\dfrac{2}{3}\)
d: \(\dfrac{1}{4}+\dfrac{1}{3}:3x=-5\)
=>\(\dfrac{1}{3}:3x=-5-\dfrac{1}{4}=-\dfrac{21}{4}\)
=>\(3x=\dfrac{1}{3}:\dfrac{-21}{4}=\dfrac{1}{3}\cdot\dfrac{4}{-21}=\dfrac{-4}{63}\)
=>\(x=-\dfrac{4}{63}:3=-\dfrac{4}{189}\)
e: \(2x^2-72=0\)
=>\(2x^2=72\)
=>\(x^2=36\)
=>\(\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
f: \(\left(\dfrac{3}{5}x-0,75\right):\dfrac{3}{7}=2\dfrac{4}{5}\)
=>\(\left(\dfrac{3}{5}x-0,75\right):\dfrac{3}{7}=\dfrac{14}{5}\)
=>\(\dfrac{3}{5}x-0,75=\dfrac{14}{5}\cdot\dfrac{3}{7}=\dfrac{6}{5}\)
=>\(\dfrac{3}{5}x=\dfrac{6}{5}+\dfrac{3}{4}=\dfrac{39}{20}\)
=>\(x=\dfrac{39}{20}:\dfrac{3}{5}=\dfrac{39}{20}\cdot\dfrac{5}{3}=\dfrac{13}{4}\)
g: \(2x+\dfrac{3}{10}=1\dfrac{5}{6}\cdot\dfrac{6}{11}\)
=>\(2x+\dfrac{3}{10}=\dfrac{11}{6}\cdot\dfrac{6}{11}=1\)
=>\(2x=\dfrac{7}{10}\)
=>\(x=\dfrac{7}{20}\)
h: \(2\dfrac{1}{4}:\left(x-7\dfrac{1}{3}\right)=-1,5\)
=>\(\dfrac{9}{4}:\left(x-\dfrac{22}{3}\right)=-\dfrac{3}{2}\)
=>\(x-\dfrac{22}{3}=\dfrac{-9}{4}:\dfrac{3}{2}=-\dfrac{9}{4}\cdot\dfrac{2}{3}=\dfrac{-3}{2}\)
=>\(x=-\dfrac{3}{2}+\dfrac{22}{3}=\dfrac{35}{6}\)

\(\left(2x+2\right)^2=64\)
\(\Rightarrow\left(2x+2\right)^2=\left(\pm8\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}2x+2=8\\2x+2=-8\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=6\\2x=-10\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Mà x là số tự nhiên nên \(x=3\).
Vậy \(x=3\).
Ta có
(2.x+2)2=64=82=(-8)2
=> 2.x+2 = 8 =(-8)
\(\left[{}\begin{matrix}2.x+2=8\\2.x+2=-8\end{matrix}\right.\) => \(\left[{}\begin{matrix}2x=6\\2x=-10\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
mà x là số tự nhiên nên x =3
Vậy x=3


Câu 1: B
Câu 2: A
Câu 3: B
Câu 4: C
Câu 5: D
Câu 6: A
Câu 7: \(\dfrac{x+2}{6}=\dfrac{-15}{2}\)
=>\(\dfrac{x+2}{6}=\dfrac{-45}{6}\)
=>x+2=-45
=>x=-47
=>Chọn C
Câu 8: B
Câu 9: C
Câu 10: A
Câu 11: \(x\cdot\dfrac{3}{4}=\dfrac{7}{8}\)
=>\(x=\dfrac{7}{8}:\dfrac{3}{4}=\dfrac{7}{8}\cdot\dfrac{4}{3}=\dfrac{28}{24}=\dfrac{7}{6}\)
=>Chọn C
Câu 12: C
Câu 13: D
Câu 14; C
Câu 15: A
Câu 16: D
II: Tự luận:
Bài 2:
a: \(3\dfrac{1}{3}x+16=13,25\)
=>\(x\cdot\dfrac{10}{3}=13,25-16=-2,75\)
=>\(x=-\dfrac{11}{4}:\dfrac{10}{3}=-\dfrac{11}{4}\cdot\dfrac{3}{10}=\dfrac{-33}{40}\)
b: \(x-43=\left(57-x\right)-50\)
=>x-43=7-x
=>2x=50
=>x=25

Số đoạn thẳng vẽ được là:
\(24\times\dfrac{\left(24-1\right)}{2}=12\times23=276\left(đoạn\right)\)

a: ĐKXĐ: \(x\ne\dfrac{1}{2}\)
Để \(\dfrac{5x}{2x-1}\) là số hữu tỉ thì \(2x-1\ne0\)
=>\(x\ne\dfrac{1}{2}\)
b: ĐKXĐ: x<>-1
Để \(\dfrac{x+5}{2x+2}\) là số nguyên thì \(x+5⋮2x+2\)
=>\(2x+10⋮2x+2\)
=>\(2x+2+8⋮2x+2\)
=>\(8⋮2x+2\)
mà 2x+2 chẵn
nên \(2x+2\in\left\{2;-2;4;-4;8;-8\right\}\)
=>\(x\in\left\{0;-2;1;-3;3;-5\right\}\)
c: ĐKXĐ: x<>-2
Để \(\dfrac{x^2+2x+3}{x+2}\) là số nguyên thì \(x^2+2x+3⋮x+2\)
=>\(x\left(x+2\right)+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)







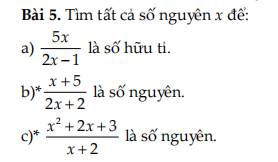
Lời giải:
Phản chứng, giả sử $a$ không cắt $b$. Suy ra $a\parallel b$
Mà: $a\perp Ox$
$\Rightarrow b\perp Ox$
Mà $b\perp Oy$
$\Rightarrow Ox\parallel Oy$
Điều này vô lý do $Ox$ cắt $Oy$ (bằng chứng là $\widehat{xOy}$ là góc nhọn)
Vậy điều giả sử là sai. Suy ra $a$ cắt $b$
100% ra kitsune