Câu 1. cho tứ giác ABCD gọi E,F,I thứ tự là trung điểm của AD,BC,AC . Chứng minh
a) EI//CD , IF // AB b) 2EF<=AB+CD
Câu 2. cho tam giác ABC, các trung tuyến BD và CE gặp nhau tại G . Gọi I và K lần lượt là trung điểm của BG,CG
a) chứng minh IK // DE và IK=DE
b) đường thẳng IK cắt AB,AC tại M và N. Qua G vẽ đường thẳng song song với BC cắt AB và AC lần lượt ở P và Q. chứng minh:DE=3MI,MI=KN,PG=GQ
Câu 3. cho hình thangABCD (AB // CD và AB<CD). Gọi E và F lần lượt là trung điểm của AC và BD. Đường thẳng EF cắt BD,AC lần lượt ở I và K
a) chứng minh: IK=CD−AB2CD−AB2
b) cho AB=4cm,CD=7CM. Tính EI,KF,IK
Mình đang cần gấp, mong các bạn giải giúp mk,mọi người trình bày rõ lời giải để mk hiểu nhé! THANK

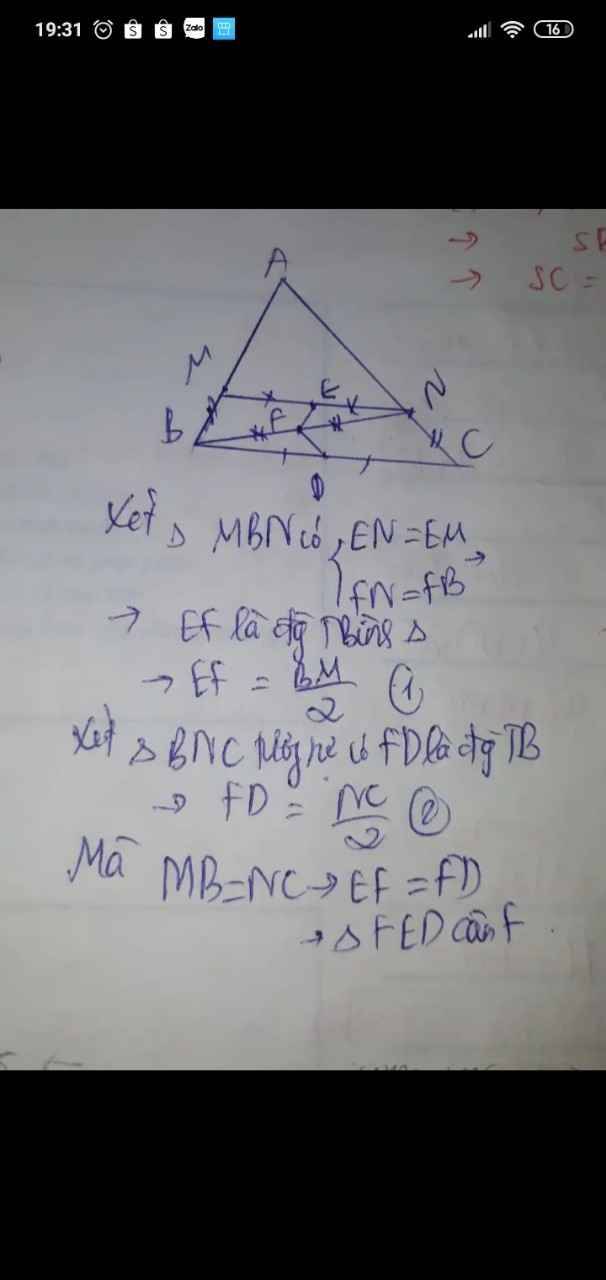
câu 3. a) chứng minh IK =\(\frac{CD-AB}{2}\)