Lời giải:

Có n điểm. Đối với mỗi điểm được xét, ta nối với n-1 điểm còn lại thì được $n-1$ đường thẳng.

Áp dụng cho n điểm, ta được $n(n-1)$ đường thẳng.

Xem xét trong $n(n-1)$ đường thẳng này, mỗi đường thẳng sẽ được tính lặp lại 2 lần (kiểu có 2 điểm A, B thì đường thẳng AB được tính 1 lần, BA được tính 1 lần nhưng bản chất chỉ là 1 đường thẳng) 

$\Rightarrow$ có $n(n-1):2$ đường thẳng được tạo ra.

Có:

$n(n-1):2=21$

$n(n-1)=2.21=42=6.7$

$\Rightarrow n=7$

Đây là dạng toán nâng cao chuyên đề điểm và đoạn thẳng, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay olm sẽ hướng dẫn em làm dạng này như sau:

     +    Xét các điểm không thẳng hàng ta có:

Số điểm không thẳng hàng là:  30 - 11  = 19 (điểm)

Cứ 1 điểm sẽ tạo với 19 -  1 điểm còn lại 19 -  1 đường thẳng.

Với 19 điểm sẽ tạo được: (19 - 1) x 19 đường thẳng.

Theo cách tính trên mỗi đường thẳng được tính hai lần.

Vậy thực tế số đường thẳng được tạo là:

      (19 - 1) x 19 : 2 = 171 (đường thẳng)

+ Xét các điểm thẳng hàng ta có: 

      Vì 11 điểm thẳng hàng với nhau nên qua 11 điểm ta chỉ có thể dựng được 1 đường thẳng và chỉ 1 đường thẳng đó là đường thẳng d.

Xét 19 điểm không trên đường thẳng d với 11 điểm nằm trên đường thẳng d ta có:

Cứ 1 điểm nằm ngoài đường thẳng d ta dựng được với 11 điểm nằm trên đường thẳng d số đường thẳng là: 11 đường thẳng.

Với 19 điểm nằm ngoài đường thẳng d ta dựng được với 11 điểm nằm trên đường thẳng d số đường thẳng là: 

      11 x 19 = 209 (đường thẳng)

Từ những lập luận trên ta có tất cả số đường thẳng có thể dựng được là: 171 + 1 + 209 = 281 (đường thẳng)

Kết luận:.. 

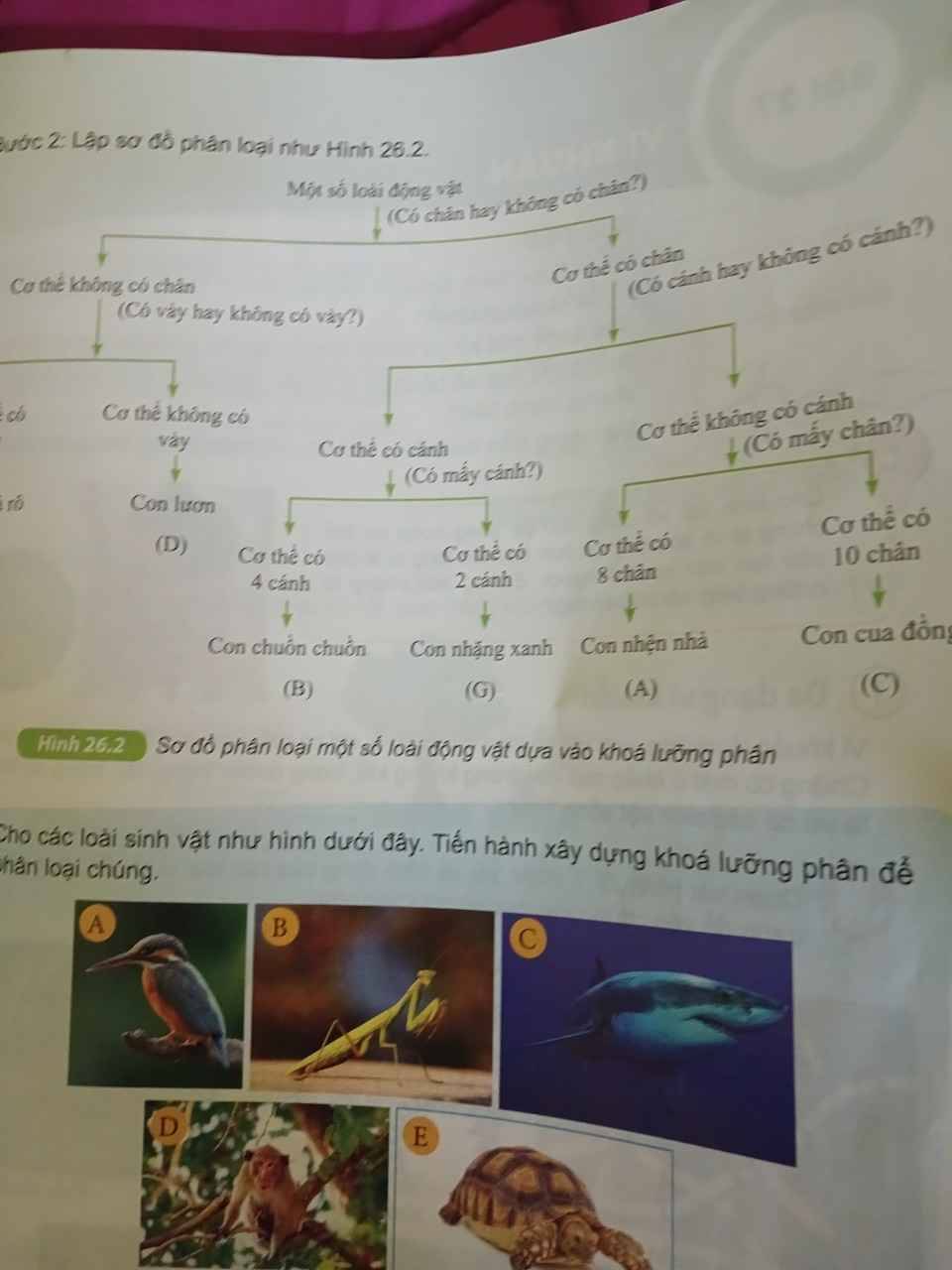
có cánh và ko nha 

có cánh là chuồn và nhặng xanh rồi tiếp là

có mấy cánh

ko cánh là cá rô phi và cua đồng

có chân và ko  

đây là ví dụ: 

3 Bước cần làm khi giải toán có lời văn.

1. Đọc kỹ đề bài

2. Phân tích bài

3. Bắt đầu giải bài dựa theo những gì đề bài cho

Đọc kĩ đề, tóm tắt đề bài đầy đủ, chi tiết, suy nghĩ kĩ đề, giải bài cẩn thận, không vội vàng.

8 bit

1 byte = 8 bits

Bài 5:

Muốn làm bài quy đồng mẫu số thì cần tìm BCNN của các mẫu. Với mẫu $a$ và BCNN là $ak$ thì ta nhân cả tử với mẫu với $k$ để quy đồng.

a. \(\frac{1}{4}=\frac{3}{12}; \frac{5}{6}=\frac{10}{12}\)

b. $\frac{-18}{240}=\frac{-18}{240}; \frac{7}{-80}=\frac{-21}{240}$
c. $\frac{-3}{16}=\frac{-9}{48}; \frac{5}{24}=\frac{10}{48}$

d. $\frac{24}{-143}=\frac{-24}{143}; \frac{6}{13}=\frac{-66}{143}$

e. $\frac{-3}{16}=\frac{-9}{48}; \frac{5}{24}=\frac{10}{48}; \frac{-21}{56}=\frac{-3}{8}=\frac{-18}{48}$

f. $\frac{11}{18}=\frac{22}{36}; \frac{-5}{9}=\frac{-20}{36}; \frac{-8}{12}=\frac{-24}{36}$

g.

$\frac{15}{-25}=\frac{-3}{5}=\frac{-9}{15}$

$\frac{-4}{15}=\frac{-4}{15}$

$\frac{1}{3}=\frac{5}{15}$

h.

$\frac{5}{21}=\frac{20}{84}$

$\frac{3}{-28}=\frac{-3}{28}=\frac{-9}{84}$

$\frac{-45}{108}=\frac{-5}{12}=\frac{-35}{84}$

cho hỗn hợp đó vào trong 1 cái xát có lỗ bé hơn muối,vì cát bé hơn muối rất nhiều nên cát sẽ rơi ra và hoàn thành 

Hòa tan hỗn hợp muối ăn và cát vào nước, muối ăn tan trong nước tạo dung dịch muối,cát không tan trong nước ta lọc cát ra khỏi dung dịch được dung dịch nước muối, đem cô cạn nước muối thu được muối.

Bài 3: 

A = \(\dfrac{3}{n+4}\)  

a; A là phân số khi và khi n + 4 ≠ 0 ⇒ n ≠ - 4

Vậy A là phân số khi n ≠ - 4

b; A = \(\dfrac{3}{n+4}\) (đk n ≠ - 4)

   A  \(\in\) Z ⇔ 3 ⋮ n + 4

     n  + 4  \(\in\) Ư(3) = {-3; -1; 1; 3}

Lập bảng ta có:

Kết luận theo bảng trên ta có:

A \(\in\) Z khi n \(\in\) {-7; -5; -3; -1}

Bài 4:

B = \(\dfrac{n+2}{n-3}\)

a; B là phân số khi và chỉ khi 

    n -  3  ≠ 0

    n \(\ne\) 3

Vậy B là phân số thì n \(\ne\) 3

b; B = \(\dfrac{n+2}{n-3}\) (n \(\ne\) 3)

    Để B \(\in\) Z thì n + 2  ⋮ n  -3

                        n - 3 + 5  ⋮ n - 3

                                  5   ⋮ n  -3

n - 3 \(\in\) Ư(5) = {-5; -1; 1; 5}

Lập bảng ta có:

Kết luận:  theo bảng trên ta có A là số nguyên khi n \(\in\){-2; 2; 4;8}

Bài 1:

Xét 3 điểm không thẳng hàng ta có:

Cứ 1 điểm tạo với 3 -  1 điểm còn lại  3 - 1 đường thẳng.

Với 3 điểm sẽ tạo được số đường thẳng là: (3- 1) x 3 đường thẳng

Theo cách tính trên mỗi đường thẳng được tính hai lần

Vậy thực tế số đường thẳng là: (3 - 1) x 3 : 2  = 3 (đường thẳng)

Số điểm thẳng hàng là: 20 - 3  = 17 (điểm)

Vì 17 điểm này thẳng hàng với nhau nên qua 17 điểm này ta chỉ kẻ được một đường thẳng duy nhất là đường thẳng d

Xét 3 điểm nằm ngoài đường thẳng d với 17 điểm nằm trên đường thẳng d ta có:

Cứ 1 điểm nằm ngoài đường thẳng d ta có thể kẻ được với 17 điểm nằm trên đường thẳng d số đường thẳng là 17 đường thẳng.

Với 3 điểm nằm ngoài đường thẳng d ta có thể kẻ được với 17 điểm trên đường thẳng d số đường thẳng là: 

 17 x 3  = 51 (đường thẳng)

Từ các lập luận trên ta có Tất cả số đường thẳng tạo được là:

       3 + 1 + 51 = 55 (đường thẳng)

Đs..

Bài 2:

+ Xét số điểm không thẳng hàng

Số điểm không thẳng hàng là: 

      20 -  5  = 15 (điểm)

Cứ 1 điểm sẽ tạo với 15 - 1 điểm còn lại 15 - 1 đường thẳng

Với 15 điểm ta sẽ tạo được số đường thẳng là: (15 - 1) x 15 đường thẳng.

Theo cách tính trên mỗi đường thẳng sẽ được tính hai lần. Vậy thực tế số đường thẳng là:

             (15  - 1) x 15 : 2  =  105 (đường thẳng)

Xét 5 điểm thẳng hàng, vì 5 điểm này thẳng hàng với nhau nên qua 5 điểm đó ta chỉ kẻ được duy nhất một đường thẳng là đường thẳng d.

Xét  15 điểm nằm ngoài đường thẳng d với 5 điểm nằm trên đường thẳng d ta có:

Cú 1 điểm nằm ngoài đường thẳng d tạo với 5 điểm nằm trên đường thẳng d số đường thẳng là 5 đường thẳng.

Với 15 điểm nằm ngoài đường thẳng d sẽ tạo được với 5 điểm trên đường thẳng d số đường thẳng là: 

5 x 15  =  75 (đường thẳng)

Từ những lập luận trên ta có số đường thẳng được tạo sẽ là:

  105 + 1 + 75 = 181  (đường thẳng)

đs...