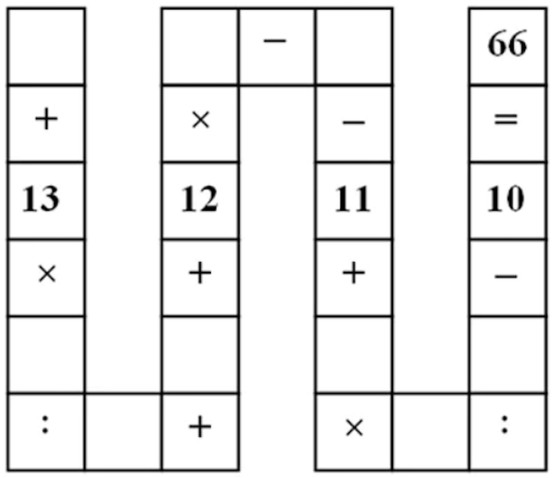
Điền các số từ 1 - 9 (không trùng lặp) vào ô trống trên bảng tính hình rắn phía trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
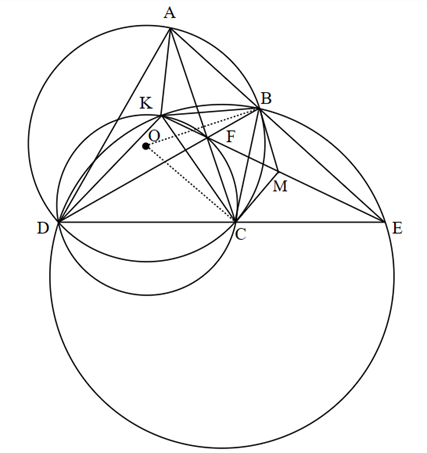
a) Vì điểm K nằm trên đường tròn ngoại tiếp ΔBDE nên tứ giác DKBE nội tiếp đường tròn
Suy ra ˆBEK=ˆBDK𝐵𝐸𝐾^=𝐵D𝐾^ (2 góc nội tiếp cùng chắn cung BK)
Hay ˆAEK=ˆFDK𝐴𝐸𝐾^=FD𝐾^
Vì tứ giác DKFC nội tiếp đường tròn nên ˆFCK=ˆFDK𝐹𝐶𝐾^=FD𝐾^
Suy ra ˆAEK=ˆFCK𝐴𝐸𝐾^=FC𝐾^, hay ˆAEK=ˆACK𝐴𝐸𝐾^=AC𝐾^
Do đó tứ giác AKCE nội tiếp đường tròn
Suy ra ˆKAE+ˆKCE=180∘𝐾AE^+𝐾𝐶𝐸^=180∘
Mà ˆKCD+ˆKCE=180∘𝐾𝐶D^+𝐾𝐶𝐸^=180∘ (hai góc kề bù)
Do đó ˆKAE=ˆKCD𝐾AE^=𝐾𝐶D^ hay ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^
Do tứ giác BKDE nội tiếp đường tròn nên ˆKDE+ˆKBE=180∘𝐾𝐷E^+𝐾𝐵𝐸^=180∘
Mà ˆKBA+ˆKBE=180∘𝐾𝐵𝐴^+𝐾𝐵𝐸^=180∘ (hai góc kề bù)
Do đó ˆKDE=ˆKBA𝐾𝐷E^=𝐾𝐵𝐴^ hay ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^
Xét ΔDKC và ΔBKA có:
ˆKBA=ˆKDCKBA^=𝐾𝐷𝐶^ (chứng minh trên)
ˆKAB=ˆKCD𝐾AB^=𝐾𝐶D^ (chứng minh trên)
Suy ra (g.g)
Do đó KCKA=KDKB𝐾𝐶𝐾A=𝐾D𝐾𝐵
Hay KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵
Ta có: ˆBKD=ˆDKC+ˆBKC𝐵𝐾D^=𝐷𝐾𝐶^+𝐵𝐾𝐶^; ˆAKC=ˆBKA+ˆBKC𝐴𝐾𝐶^=𝐵𝐾𝐴^+𝐵𝐾𝐶^
Mà ˆDKC=ˆBKA𝐷𝐾𝐶^=𝐵𝐾A^, suy ra ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^
Xét ΔKBD và ΔKAC có:
ˆDKB=ˆCKA𝐷𝐾𝐵^=𝐶𝐾A^ (chứng minh trên)
KCKD=KAKB𝐾𝐶𝐾𝐷=𝐾𝐴𝐾𝐵 (chứng minh trên)
Suy ra (c.g.c)
Do đó ˆKBD=ˆKAC𝐾𝐵D^=𝐾𝐴𝐶^
Hay ˆKBF=ˆKAF𝐾𝐵𝐹^=𝐾𝐴𝐹^
Suy ra tứ giác AKFB nội tiếp đường tròn
Do đó ˆBKF=ˆBAF𝐵𝐾𝐹^=BAF^ (2 góc nội tiếp chắn cung BF)
Suy ra ˆBKF=ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^=𝐵D𝐶^ (do ˆBAC,ˆBDC𝐵𝐴𝐶^,𝐵D𝐶^ cùng chắn cung BC) (1)
Ta có: ˆBDC=ˆFDC=ˆFKC𝐵D𝐶^=𝐹D𝐶^=𝐹𝐾𝐶^ (cùng chắn cung FC) (2)
Xét ΔBMC có ˆMBC+ˆMCB+ˆBMC=180∘𝑀𝐵𝐶^+𝑀𝐶𝐵^+𝐵𝑀𝐶^=180∘ (tổng ba góc trong một tam giác)
Mà ˆMBC=ˆBAC,ˆMCB=ˆBDC𝑀𝐵𝐶^=𝐵𝐴𝐶^,𝑀𝐶𝐵^=𝐵D𝐶^(Góc tạo bởi tiếp tuyến và dây cung)
Suy ra ˆBAC+ˆBDC+ˆBMC=180∘𝐵𝐴𝐶^+𝐵𝐷𝐶^+𝐵𝑀𝐶^=180∘ (3)
Từ (1); (2) và (3) suy ra ˆBKF+ˆFKC+ˆBMC=180∘𝐵𝐾𝐹^+𝐹𝐾𝐶^+𝐵𝑀𝐶^=180∘
Hay ˆBKC+ˆBMC=180∘𝐵𝐾𝐶^+𝐵𝑀𝐶^=180∘
Do đó tứ giác BKCM nội tiếp đường tròn
b) Ta có ˆBKF=ˆBDC𝐵𝐾𝐹^=𝐵D𝐶^ (chứng minh câu a)
Suy ra ˆBKF=ˆBDE=ˆBKE𝐵𝐾𝐹^=𝐵DE^=𝐵𝐾𝐸^ (Do tứ giác DKBE nội tiếp đường tròn)
Mà 2 điểm F và E nằm cùng phía so với BK
Suy ra 3 điểm K; F; E thẳng hàng
Hay F nằm trên KE (*)
Vì ˆBKF=ˆBAC,ˆCKF=ˆBDC,ˆBAC=ˆBDC𝐵𝐾𝐹^=𝐵𝐴𝐶^,𝐶𝐾𝐹^=𝐵D𝐶^,𝐵𝐴𝐶^=𝐵D𝐶^
Nên ˆBKF=ˆCKF𝐵𝐾𝐹^=𝐶𝐾𝐹^
Suy ra ˆBKE=ˆCKE𝐵𝐾𝐸^=𝐶𝐾𝐸^ (Do K; F; E thẳng hàng)
Do đó KE là phân giác của ˆBKC𝐵𝐾𝐶^ (4)
Xét (O) có MB, MC là 2 tiếp tuyến cắt nhau tại M
Nên MB = MC
Do đó tam giác MBC cân tại M
Suy ra ˆMBC=ˆMCB𝑀𝐵𝐶^=𝑀𝐶𝐵^
Xét tứ giác BKCM nội tiếp đường tròn có ˆMBC=ˆMKC,ˆMCB=ˆMKB𝑀𝐵𝐶^=𝑀𝐾𝐶^,𝑀𝐶𝐵^=𝑀𝐾𝐵^
Suy ra ˆMKC=ˆMKB𝑀𝐾𝐶^=𝑀𝐾𝐵^
Do đó KM là phân giác của ˆBKC𝐵𝐾𝐶^ (5)
Từ (4) và (5) suy ra 3 điểm K; M; E thẳng hàng hay M nằm trên KE (**)
Từ (*) và (**) suy ra 3 điểm E; M; F thẳng hàng
Vậy 3 điểm E; M; F thẳng hàng.