ước lớn hơn 7 của 30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
`(3x-6)^2022>=0` với mọi x
`(5y+10)^2024>=0` với mọi y
`=>(3x-6)^2022+(5y+10)^2024>=0` với mọi x,y
Mặt khác: `(3x-6)^2022+(5y+10)^2024)<=0` với mọi x,y
Dấu "=" xảy ra: `3x-6=0` và `5y+10=0`
`<=>3x=6` và `5y=-10`
`<=>x=6/3=2` và `y=-10/5=-2`

\(A=1^2-2^2+3^2-4^2+...+2023^2-2024^2+2025^2\\ =\left(1+2\right)\left(1-2\right)+\left(3+4\right)\left(3-4\right)+\left(2023-2024\right)\left(2023+2024\right)\\ =-3-7-11-...-4047+2025^2\\ =-\left(3+7+11+..+4047\right)+2025^2\)
Xét tổng: `3+7+11+...+4047`
Số lượng số hạng: `(4047-3):4+1=1012`
Tổng: `(4047+3)*1012/2=2049300`
`=>A=-2049300+2025^2`
`=>A=-2049300+4100625`
`=>A=2051325`

Cạnh của hình vuông là:
`35:4=8,75(cm)`
Diện tích hình vuông đó là:
`8,75 xx 8,75 = 76,5625 (cm^2)`
ĐS: ...

\(\left(3x-3\right)^2+\left(4y+2\right)^2=0\)
Ta có:
`(3x-3)^2>=0` với mọi x
`(4y+2)^2>=0` với mọi x
`=>(3x-3)^2+(4y+2)^2>=0` với mọi x,y
Mặt khác: `(3x-3)^2+(4y+2)^2=0`
Dấu "=" xảy ra: `3x-3=0` và `4y+2=0`
`=>3x=3` và `4y=-2`
`=>x=3/3=1` và `y=-2/4=-1/2`

\(VT=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\cdot\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\\ =\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\cdot\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\\ =\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)\\ =1-\left(\sqrt{a}\right)^2\\ =1-a=VP\)

Giá tiền hai món mà Hà mua là:
`30000 - 2000 = 28000 ` (đồng)
Giá bành mì là:
`(28000 + 12000) : 2 = 20 000 ` (đồng)
Giá hộp sữa là:
`20000 - 12000 = 8000` (đồng)
Đáp số: ...

Bài 5:
\(a,\dfrac{11}{24}-\dfrac{5}{41}+\dfrac{13}{24}+0,5-\dfrac{36}{41}\\ =\left(\dfrac{11}{24}+\dfrac{13}{24}\right)+\left(\dfrac{-5}{41}-\dfrac{36}{41}\right)+0,5\\ =\dfrac{24}{24}-\dfrac{41}{41}+\dfrac{1}{2}\\ =1-1+\dfrac{1}{2}\\=\dfrac{1}{2}\\ b,16\cdot\dfrac{3}{5}\cdot\dfrac{-1}{3}-13\dfrac{3}{5}\cdot\dfrac{-1}{3}\\ =\dfrac{-1}{3}\cdot\left(16+\dfrac{3}{5}-13-\dfrac{3}{5}\right)\\ =\dfrac{-1}{3}\cdot3\\ =-1\)
Bài 2:
\(\left(\dfrac{-4}{7}\right)^{25}:\left(\dfrac{-4}{7}\right)^{23}\\ =\left(\dfrac{-4}{7}\right)^{25-23}\\ =\left(\dfrac{-4}{7}\right)^2\\ =\dfrac{16}{49}\\ b,\dfrac{15}{60}+\dfrac{12}{19}+\dfrac{2}{9}-\dfrac{10}{8}+\dfrac{-31}{19}\\ =\dfrac{1}{4}+\left(\dfrac{12}{19}-\dfrac{31}{19}\right)+\dfrac{2}{9}-\dfrac{5}{4}\\ =\left(\dfrac{1}{4}-\dfrac{5}{4}\right)+\dfrac{-19}{19}+\dfrac{2}{9}\\ =-1-1+\dfrac{2}{9}\\ =\dfrac{2}{9}-2\\ =-\dfrac{16}{9}\)

Nếu \(a\ne3\Rightarrow\) tập B có phần tử 3 nhưng tập A ko có \(\Rightarrow A\ne B\) (ko thỏa mãn)
\(\Rightarrow a=3\)
Khi đó \(A=\left\{5;1;3\right\}\) ; \(B=\left\{5;3;b\right\}\)
\(\Rightarrow b=1\)

Do n ϵ Z ⇒ A ϵ Z.
\(A=\dfrac{2\left(n-1\right)+5}{n-1}\)
\(A=2+\dfrac{5}{n-1}\)
\(\Rightarrow5⋮\left(n-1\right)\)
\(\Rightarrow\left(n-1\right)\in\left\{1;-1;5;-5\right\}\)
Ta có bảng giá trị:
| n - 1 | 1 | -1 | 5 | -5 |
| n | 2 | 0 | 6 | -4 |
| A | 7 | -3 | 3 | 1 |
⇒ Để A đạt GTNN thì A = -3 → n = 0
GTLN thì A = 7 → n = 2


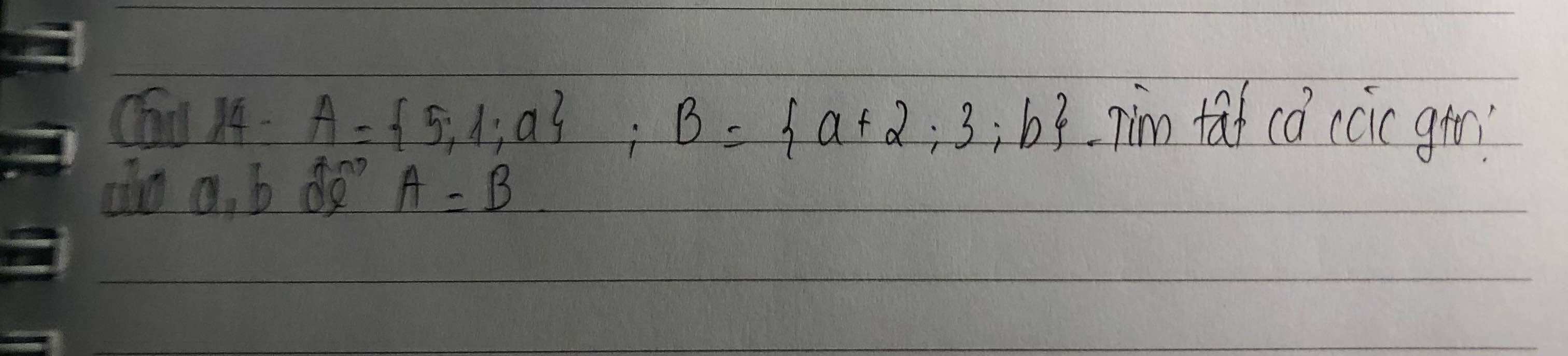
Vì là ước không bắt buộc là só nguyên tố nên các ước lớn hơn của 30 là: 10; 15; 30.