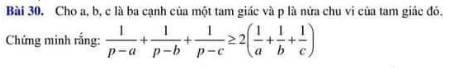
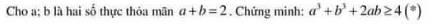
a) Diện tích xung quanh bể:

(12,5 + 7,5) × 2 × 5 = 200 (dm²)

Diện tích đáy bể:

12,5 × 7,5 = 93,75 (dm²)

Diện tích kính dùng làm bể cá:

200 + 93,75 = 293,75 (dm²)

b) Số lít nước cần dùng để nuôi cá:

12,5 × 7,5 × 5 × 3/4 = 351,5625 (dm³) = 351,5625 (l)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:

$\frac{1}{p-a}+\frac{1}{p-b}\geq \frac{4}{p-a+p-b}=\frac{4}{2p-a-b}=\frac{4}{c}$

$\frac{1}{p-b}+\frac{1}{p-c}\geq \frac{4}{p-b+p-c}=\frac{4}{a}$
$\frac{1}{p-a}+\frac{1}{p-c}\geq \frac{4}{p-a+p-c}=\frac{4}{b}$

Cộng theo vế 3 BĐT trên và thu gọn thì:

$\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\geq 2(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$

Ta có đpcm

Dấu "=" xảy ra khi $a=b=c$

Lời giải:

Ta có:

$a^3+b^3+2ab-4=(a+b)^3-3ab(a+b)+2ab-4$

$=2^3-6ab+2ab-4=4-4ab=(a+b)^2-4ab=a^2+b^2-2ab=(a-b)^2\geq 0$ với mọi $a,b\in\mathbb{R}$

$\Rightarrow a^3+b^3+2ab\geq 4$

Ta có đpcm

Dấu "=" xảy ra khi $a=b=1$

     \(\dfrac{3}{x}\) = \(\dfrac{4}{12}\) (đk \(x\ne\) 0)

      \(x\) =  3 : \(\dfrac{4}{12}\)

       \(x\) = 9

Vậy \(x=9\) 

a: Xét ΔAMB và ΔDMC có

MA=MD

\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)

MB=MC

Do đó: ΔAMB=ΔDMC

b: Ta có: ΔAMB=ΔDMC

=>\(\widehat{MAB}=\widehat{MDC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AB//DC

Ẩn của phương trình đâu vậy em?

b: \(10A=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)

\(10B=\dfrac{10^{10}+10}{10^{10}+1}=1+\dfrac{9}{10^{10}+1}\)

Vì \(10^9+1< 10^{10}+1\)

nên \(\dfrac{9}{10^9+1}>\dfrac{9}{10^{10}+1}\)

=>\(1+\dfrac{9}{10^9+1}>1+\dfrac{9}{10^{10}+1}\)

=>10A>10B

=>A>B

Đề thiếu em nha

a;

A = \(\dfrac{2}{x-1}\) (đk 1≠ \(x\) \(\in\) z)

A \(\in\) Z ⇔ 2 ⋮ \(x-1\)

\(x-1\) \(\in\) {-2; -1; 1; 2}

Lập bảng ta có:

Theo bảng trên ta có: \(x\) \(\in\) {-1; 0; 2; 3}

Vậy để A   = \(\dfrac{2}{x-1}\) có giá trị nguyên thì \(x\in\) {-1; 0; 2; 3}