Có một cái sân hình chữ nhật chu vi 8 cm,người ta mở rộng về bên phải 3 m và mở rộng về bên trái 5 m.Hỏi sau khi mở rộng chu vi sân là bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2
a; \(\dfrac{-5}{7}\) - \(\dfrac{3}{14}\)
= \(\dfrac{-10}{14}\) - \(\dfrac{3}{14}\)
= \(\dfrac{-13}{14}\)
b; \(\dfrac{5}{6}+\dfrac{1}{6}:\left(-6\right)+\left(-4\right)\)
= \(\dfrac{5}{6}\) - \(\dfrac{1}{36}\) - 4
= \(\dfrac{30}{36}-\dfrac{1}{36}-\dfrac{144}{36}\)
= \(\dfrac{-115}{36}\)
Bài 2
c; - \(\dfrac{4}{3}.\dfrac{7}{6}+\dfrac{-4}{3}.\dfrac{5}{6}\) + \(\dfrac{-5}{6}\)
= - \(\dfrac{4}{3}.\left(\dfrac{7}{6}+\dfrac{5}{6}\right)\) - \(\dfrac{5}{6}\)
= - \(\dfrac{4}{3}\). 2 - \(\dfrac{5}{6}\)
= - \(\dfrac{8}{3}-\dfrac{5}{6}\)
= \(\dfrac{-16}{6}-\dfrac{5}{6}\)
= - \(\dfrac{7}{2}\)

a) Diện tích xung quanh bể:
(12,5 + 7,5) × 2 × 5 = 200 (dm²)
Diện tích đáy bể:
12,5 × 7,5 = 93,75 (dm²)
Diện tích kính dùng làm bể cá:
200 + 93,75 = 293,75 (dm²)
b) Số lít nước cần dùng để nuôi cá:
12,5 × 7,5 × 5 × 3/4 = 351,5625 (dm³) = 351,5625 (l)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
$\frac{1}{p-a}+\frac{1}{p-b}\geq \frac{4}{p-a+p-b}=\frac{4}{2p-a-b}=\frac{4}{c}$
$\frac{1}{p-b}+\frac{1}{p-c}\geq \frac{4}{p-b+p-c}=\frac{4}{a}$
$\frac{1}{p-a}+\frac{1}{p-c}\geq \frac{4}{p-a+p-c}=\frac{4}{b}$
Cộng theo vế 3 BĐT trên và thu gọn thì:
$\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\geq 2(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c$

Lời giải:
Ta có:
$a^3+b^3+2ab-4=(a+b)^3-3ab(a+b)+2ab-4$
$=2^3-6ab+2ab-4=4-4ab=(a+b)^2-4ab=a^2+b^2-2ab=(a-b)^2\geq 0$ với mọi $a,b\in\mathbb{R}$
$\Rightarrow a^3+b^3+2ab\geq 4$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=1$

\(\dfrac{3}{x}\) = \(\dfrac{4}{12}\) (đk \(x\ne\) 0)
\(x\) = 3 : \(\dfrac{4}{12}\)
\(x\) = 9
Vậy \(x=9\)

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔDMC
b: Ta có: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC


b: \(10A=\dfrac{10^9+10}{10^9+1}=1+\dfrac{9}{10^9+1}\)
\(10B=\dfrac{10^{10}+10}{10^{10}+1}=1+\dfrac{9}{10^{10}+1}\)
Vì \(10^9+1< 10^{10}+1\)
nên \(\dfrac{9}{10^9+1}>\dfrac{9}{10^{10}+1}\)
=>\(1+\dfrac{9}{10^9+1}>1+\dfrac{9}{10^{10}+1}\)
=>10A>10B
=>A>B

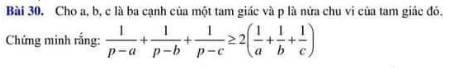
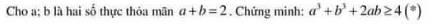

Lời giải:
** Sửa 8 cm thành 8 m
Sau khi mở rộng thì chu vi mới của sân là:
$8+(3+5)\times 2=24$ (m)