1/1×2+1/2×3+1/3×4+.....1/2006×2007
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



| x + \(\frac{3}{4}\)| - \(\frac{1}{4}\)= 0
| x + \(\frac{3}{4}\)| = 0 + \(\frac{1}{4}\)
| x + \(\frac{3}{4}\)| = \(\frac{1}{4}\)
x + \(\frac{3}{4}\) = - \(\frac{1}{4}\)
x + \(\frac{3}{4}\) = + \(\frac{1}{4}\)
Trường hợp 1: Trường hợp 2:
x + \(\frac{3}{4}\)= \(\frac{1}{4}\) x + \(\frac{3}{4}\)= \(\frac{-1}{4}\)
x = \(\frac{1}{4}\)- \(\frac{3}{4}\) x = \(\frac{-1}{4}\)- \(\frac{3}{4}\)
x = \(\frac{1}{4}\)+\(\frac{-3}{4}\) x = \(\frac{-1}{4}\)+\(\frac{-3}{4}\)
x = \(\frac{-2}{4}\) x = - 1
Vậy x = \(\frac{-2}{4}\); - 1

\(\left|x+\frac{3}{4}\right|-\frac{1}{4}=0\)
\(\Rightarrow\left|x+\frac{3}{4}\right|=\frac{1}{4}\)
\(\Rightarrow\orbr{\begin{cases}x-\frac{3}{4}=\frac{1}{4}\\x-\frac{3}{4}=\frac{-1}{4}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{1}{4}-\frac{3}{4}\\x=\frac{-1}{4}-\frac{3}{4}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=-1\end{cases}}\)

\(\frac{17}{6}-\left(x-\frac{7}{6}\right)=\frac{7}{4}\)
\(x-\frac{7}{6}=\frac{17}{6}-\frac{7}{4}\)
\(x-\frac{7}{6}=\frac{13}{12}\)
\(x=\frac{13}{12}+\frac{7}{6}\)
\(x=\frac{9}{4}\)
* Sai xin lỗi nhé, mình ko nhìn rõ là \(\frac{17}{6}\) hay \(\frac{11}{6}\) ;-; *
Học tốt
@Ngien

O y x n t m
a)
Theo đề ra, ta có:
\(\widehat{xOn}+\widehat{nOm}=\widehat{xOm}\)
\(\widehat{yOm}+\widehat{nOm}=\widehat{yOn}\)
Ta có \(\widehat{xOm}=\widehat{yOn}=90^o\Rightarrow\widehat{xOn}=\widehat{yOm}\)
b)
Theo đề ra, ta có: Ot là tia phân giác của \(\widehat{xOy}\Rightarrow\widehat{xOt}=\widehat{yOt}=\widehat{xOy}:2\)
Ta có:
\(\widehat{xOn}+\widehat{nOt}=\widehat{xOt}\)
\(\widehat{yOm}+\widehat{mOt}=\widehat{yOt}\)
Mà \(\widehat{xOt}=\widehat{yOt}\)và\(\widehat{xOn}=\widehat{yOm}\)
\(\Rightarrow\widehat{nOt}=\widehat{mOt}\)
Vậy Ot là tia phân giác của \(\widehat{mOn}\)
(a) Do tia On nằm giữa 2 tia Ox và Oy nên ta có ˆxOy=ˆxOn+ˆnOyxOy^=xOn^+nOy^
⇒ˆxOn=ˆxOy−900⇒xOn^=xOy^−900 hay ˆxOnxOn^ nhọn
⇒ˆxOn<ˆxOm⇒xOn^<xOm^ mà 2 tia Om và On cùng thuộc nửa mặt phẳng bờ Ox chứa Oy nên tia On nằm giữa tia Ox và tia Oy
⇒ˆxOn+ˆmOn=ˆxOm=900⇒xOn^+mOn^=xOm^=900
Tương tự ta có ˆyOm+ˆmOn=900yOm^+mOn^=900. Do đó ˆxOn=ˆyOmxOn^=yOm^ (đpcm).
(b) Ta có: ˆxOn=ˆxOy−900=12ˆxOy+ˆxOy−18002<ˆxOy2=ˆxOt<900=ˆxOmxOn^=xOy^−900=12xOy^+xOy^−18002<xOy^2=xOt^<900=xOm^Mà Om, On, Ot cùng thuộc nửa mặt phẳng bờ Ox chứa Oy nên tia Ot nằm giữa 2 tia Om và On.
⇒⇒ ˆnOt=ˆxOt−ˆxOn=ˆyOt−ˆyOm=ˆtOmnOt^=xOt^−xOn^=yOt^−yOm^=tOm^ hay Ot là phân giác ˆmOnmOn^


x : 0,25 = 9 : x
=> x^2 = 2,25
=> x = \(\orbr{\begin{cases}\sqrt{2,25}\\-\sqrt{2,25}\end{cases}}\)
Giải thích các bước giải:
Ta có: x:0,25=9:xx:0,25=9:x
⇔x0,25=9x⇔x0,25=9x
⇔x×x=9×0,25⇔x×x=9×0,25
⇔x2=94⇔x2=94
⇔x2=(32)2⇔x2=(32)2
⇔⇔ ⎡⎢ ⎢⎣x=32x=−32[x=32x=−32
Vậy x={32;−32}



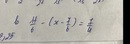

=1/1-1/2+1/2-1/3+1/3-1/4+..........+1/2006-1/2007
=1/1-1/2007
=2006/2007
OKnha bn
\(\frac{1}{1x2}\)\(+\)\(\frac{1}{2x3}\)\(+\)\(\frac{1}{3x4}\)\(+\)\(...\)\(+\)\(\frac{1}{2006x2007}\)
\(=\) \(\frac{2-1}{1x2}\)\(+\)\(\text{}\)\(\frac{3-2}{2x3}\)\(+\)\(\frac{4-3}{3x4}\)\(+\) \(....\)\(+\)\(\frac{2007-2006}{2006x2007}\).
\(=\) \(1\) \(-\)\(\frac{1}{2}\)\(+\) \(\frac{1}{2}\)\(-\)\(\frac{1}{3}\)\(+\)\(\frac{1}{3}\)\(-\)\(\frac{1}{4}\)\(+\)\(....\)\(+\)\(\frac{1}{2006}\)\(-\)\(\frac{1}{2007}\)
\(=\)\(1-\)\(\frac{1}{2007}\)
\(=\frac{2006}{2007}\)\(.\)
Mong đc k !! HT~
Nhưng bài này mk lớp 5 cũng lm đc sao lại nói là toán lớp 7 ?!