Bài 12: Một đa giác lồi có 10 đỉnh. có bao nhiêu tam giác có đúng 2 cạnh của đa giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chữ số cần lập có dạng �����‾abcde
- Nếu các chữ số không yêu cầu đôi một khác nhau:
�e có 4 cách chọn, �a có 6 cách chọn; 3 vị trí còn lại đều có 7 cách chọn
⇒⇒ có 4.6.7.7.7=82324.6.7.7.7=8232 số
- Nếu các chữ số đôi một khác nhau:
+ Nếu �=0e=0: �a có 6 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn ⇒⇒ có 6.5.4.3=3606.5.4.3=360 số
+ Nếu �≠0⇒�e=0⇒e có 3 cách chọn, a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn ⇒900⇒900 số
⇒⇒ có 900+360=1260900+360=1260 số
Lời giải:
Gọi số tự nhiên có 5 chữ số khác nhau là $\overline{abcde}$
Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 là: $5!=120$ số
Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 mà chia hết cho 5 là:
$4!.1=24$ số (do e chỉ có 1 cách chọn là số 5, 4 số còn lại hoán vị là 4!)
Số cách lập số tự nhiên có 5 chữ số khác nhau mà không chia hết cho 5:
$120-24=96$ (số)

Gọi chữ số cần lập có dạng �����‾abcde
- Nếu các chữ số không yêu cầu đôi một khác nhau:
�e có 4 cách chọn, �a có 6 cách chọn; 3 vị trí còn lại đều có 7 cách chọn
⇒⇒ có 4.6.7.7.7=82324.6.7.7.7=8232 số
- Nếu các chữ số đôi một khác nhau:
+ Nếu �=0e=0: �a có 6 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn ⇒⇒ có 6.5.4.3=3606.5.4.3=360 số
+ Nếu �≠0⇒�e=0⇒e có 3 cách chọn, a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn ⇒900⇒900 số
⇒⇒ có 900+360=1260900+360=1260 số

8.
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+4x+5}=b>0\end{matrix}\right.\) \(\Rightarrow2a^2-b^2=x^2+1\)
Pt trở thành:
\(\sqrt{2a^2-b^2}+2a=3b\)
\(\Leftrightarrow\sqrt{2a^2-b^2}=3b-2a\)
\(\Rightarrow2a^2-b^2=4a^2-12ab+9b^2\)
\(\Leftrightarrow2a^2-12ab+10b^2=0\Rightarrow\left[{}\begin{matrix}a=b\\a=5b\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x+3}=\sqrt{x^2+4x+5}\\\sqrt{x^2+2x+3}=5\sqrt{x^2+4x+5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+3=x^2+4x+5\\x^2+2x+3=25\left(x^2+4x+5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\24x^2+98x+122=0\left(vn\right)\end{matrix}\right.\)
9.
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{1+x}=a\ge0\\\sqrt{1-x}=b\ge0\end{matrix}\right.\) \(\Rightarrow a^2+2b^2=3-x=-\left(x-3\right)\)
Pt trở thành:
\(a-2b-3ab=-\left(a^2+2b^2\right)\)
\(\Leftrightarrow a-2b+a^2-3ab+2b^2=0\)
\(\Leftrightarrow a-2b+\left(a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a-b+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\a+1=b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{1+x}=2\sqrt{1-x}\\\sqrt{1+x}+1=\sqrt{1-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}1+x=4\left(1-x\right)\\x+2+2\sqrt{1+x}=1-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=3\Rightarrow x=\dfrac{3}{5}\\-1-2x=2\sqrt{1+x}\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow\left\{{}\begin{matrix}-1-2x\ge0\\\left(-1-2x\right)^2=4\left(1+x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\x^2=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow x=-\dfrac{\sqrt{3}}{2}\)
Vậy \(x=\left\{\dfrac{3}{5};-\dfrac{\sqrt{3}}{2}\right\}\)

a) Từ đồ thị, ta thấy \(A\left(0;4\right),B\left(3;0\right),C\left(0;-4\right),D\left(-3;0\right)\)
b) Ta thấy O đồng thời là trung điểm của AC và II' nên AICI' là hình bình hành \(\Rightarrow\) AI' // CI hay AI' // BC (do B, I, C thẳng hàng)
Tương tự, ta chứng minh được DI' // BC. Do đó A, I', D thẳng hàng theo tiên đề Euclide.

Lời giải:
Để 2 vecto cùng phương thì:
$\frac{m^2+m+2}{m}=\frac{4}{2}=2$ ($m\neq 0$)
$\Leftrightarrow m^2+m+2=2m$
$\Leftrightarrow m^2-m+2=0$
$\Leftrightarrow (m-0,5)^2=\frac{-7}{4}<0$ (vô lý)
Do đó không tồn tại $m$ thỏa mãn yêu cầu.

a.
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-5;-1\right)\\\overrightarrow{DC}=\left(3-x;-2-y\right)\end{matrix}\right.\)
Do ABCD là hình bình hành \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}3-x=-5\\-2-y=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)
\(\Rightarrow D\left(8;-1\right)\)
Gọi O là tâm hình bình hành \(\Rightarrow\) O là trung điểm AC
Theo công thúc trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=\dfrac{7}{2}\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(\dfrac{7}{2};\dfrac{1}{2}\right)\)
b.
Theo công thức trọng tâm: \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=2\\y_G=\dfrac{y_A+y_B+y_C}{3}=1\end{matrix}\right.\)
\(\Rightarrow G\left(2;1\right)\)
I đối xứng B qua G \(\Rightarrow G\) là trung điểm IB
\(\Rightarrow\left\{{}\begin{matrix}x_I=2x_G-x_B=5\\y_I=2y_G-y_B=0\end{matrix}\right.\) \(\Rightarrow I\left(5;0\right)\)
\(\left\{{}\begin{matrix}\dfrac{x_A+x_D+x_C}{3}=5=x_I\\\dfrac{y_A+y_D+y_C}{3}=0=y_I\end{matrix}\right.\) \(\Rightarrow I\) là trọng tâm ADC
c.
Ta có: \(S_{ABC}=\dfrac{1}{2}AB.d\left(C;AB\right)\)
\(S_{ABM}=\dfrac{1}{2}AB.d\left(M;AB\right)\)
\(S_{ABC}=3S_{ABM}\Rightarrow d\left(C;AB\right)=3d\left(M;AB\right)\)
\(\Rightarrow BM=\dfrac{1}{3}BC\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BM}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BM}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{BM}=\left(x+1;y-2\right)\)
\(\Rightarrow\left[{}\begin{matrix}\left(x+1;y-2\right)=\dfrac{1}{3}\left(4;-4\right)\\\left(x+1;y-2\right)=-\dfrac{1}{3}\left(4;-4\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(x;y\right)=\left(\dfrac{1}{3};\dfrac{2}{3}\right)\\\left(x;y\right)=\left(-\dfrac{7}{3};\dfrac{10}{3}\right)\end{matrix}\right.\)
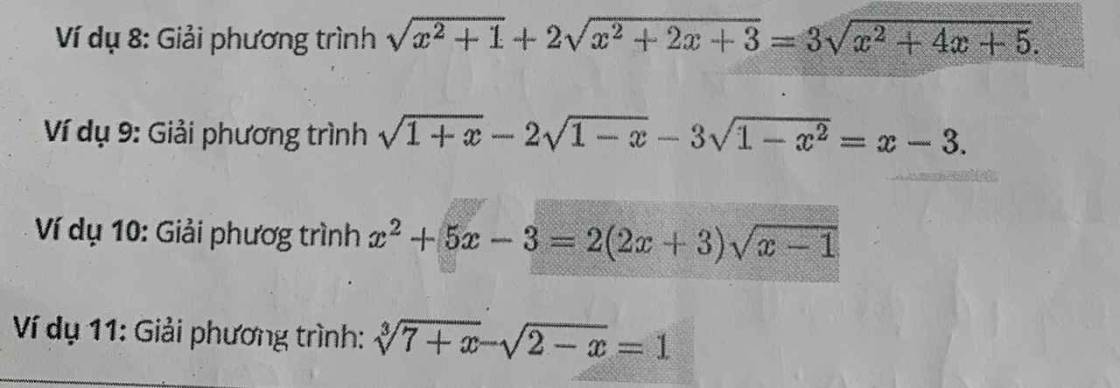
cứ mỗi đỉnh của đa giác thì sẽ tạo ra được 1 tam giác có 2 cạnh là 2 cạnh của đa giác. Mà đa giác có 10 đỉnh nên ta sẽ 10 tam giác thoả yêu câu