(x - 13 + y)² + (x - 6 - y)² ≥ 0 + 0 = 0

Vì dấu "=" xảy ra nên x - 13 + y = 0 và x - 6 - y = 0

x + y = 13 và x - y = 6

x = (13 - 6) : 2 = 3,5

y = 13 - 3,5 = 9,5

Vậy x = 3,5 và y = 9,5

(\(x\) - 13 + y)² + (\(x\) - 6 - y)² = 0

(\(x\) - 13 + y)² ≥ 0 ∀ \(x;y\)

(\(x-6-y\))² ≥ 0 ∀ \(x;y\)

⇒(\(x-13+y\))² + (\(x\) - 6- y)² = 0

⇔ \(\left\{{}\begin{matrix}x-13+y=0\\x-6-y=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x-6-y=0\\x-13+y+x-6-y=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}y=x-6\\2x=19\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{19}{2}-6\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{19}{2}\\y=\dfrac{7}{2}\end{matrix}\right.\)

|5 - \(\dfrac{2}{3}\)\(x\)| + |\(\dfrac{2}{3}\)y - 4| =0

|5 - \(\dfrac{2}{3}\)\(x\)| ≥ 0 ∀ \(x\); |\(\dfrac{2}{3}\)y - 4| ≥ 0 ∀ y

⇒ |5 - \(\dfrac{2}{3}\)\(x\)| + |\(\dfrac{2}{3}\)y - 4| = 0 ⇔ \(\left\{{}\begin{matrix}5-\dfrac{2}{3}x=0\\\dfrac{2}{3}y-4=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=\dfrac{15}{2}\\y=6\end{matrix}\right.\)

\(\dfrac{5}{6}\) - (\(\dfrac{3}{4}\) + \(\dfrac{7}{8}\) - \(x\)) = 10 - | \(\dfrac{1}{3}\) - \(\dfrac{1}{2}\)|

\(\dfrac{5}{6}\) - (\(\dfrac{13}{8}\)- \(x\)) = 10 - |-\(\dfrac{1}{6}\)|

 \(\dfrac{5}{6}\) - \(\dfrac{13}{8}\) + \(x\) = 10 + \(\dfrac{1}{6}\)

- \(\dfrac{19}{24}\) + \(x\)      = \(\dfrac{61}{6}\)

            \(x\)     = \(\dfrac{61}{6}\) + \(\dfrac{19}{24}\)

            \(x\)     = \(\dfrac{263}{24}\) 

a) 3/13 - 3/2 + 10/13

= (3/13 + 10/13) - 3/2

= 1 - 3/2

= -1/2

b) 4/7 - (-2/7) - 7/3

= 4/7 + 2/7 - 7/3

= 6/7 - 7/3

= -31/21

c) 2/3 - (-1/6) + 5/4

= 2/3 + 1/6 + 5/4

= 8/12 + 2/12 + 15/12

= 25/12

a, 3/13 - 3/2 + 10/13

= 3/13 + 10/13

= 1 - 3/2 = -1/2

b,4/7 - (-2/7) - 7/3

= 4/7 + 2/7 - 7/3

= 6/7 - 7/3

= 18/21 - 14/21

= 4/21

c, 2/3 - -1/6 +5/4 

= 2/3 + 1/16 +5/4

= 128/192 + 12/192 + 240/192

= 380/192

= 95/4 

không hiểu chỗ nào hỏi tui

Hình vẽ nào vậy em

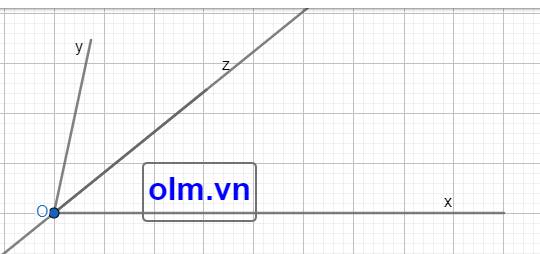
a, Trên cùng một nửa mặt phẳng có bờ là tia ox vì \(\widehat{xOy}\) > \(\widehat{xOz}\) nên Oz nằm giữa hai tia Oy và Ox.

b, \(\widehat{xOy}\) = \(\widehat{xOz}\) +  \(\widehat{zOy}\) ⇒ \(\widehat{zOy}\)  = 80⁰ -  40⁰ = 40⁰

c, Oz nằm giữa hai tia Oy và Ox và \(\widehat{zOy}\) = \(\widehat{xOz}\)  nên OZ là tia phân giác của góc xOy

\(\dfrac{x-1}{3}=\dfrac{27}{x-1}\\ \Rightarrow\left(x-1\right)^2=27\cdot3\\ \Rightarrow\left(x-1\right)^2=81\\ \Rightarrow\left(x-1\right)^2=\pm8^2\\ \Rightarrow\left[{}\begin{matrix}x-1=8\\x-1=-8\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=9\\x=-7\end{matrix}\right.\)

Giúp mình với, mình cần gấp

Thời gian Lâm tới nhà bà:

\(3:9=\dfrac{1}{3}\left(h\right)\)

\(\dfrac{1}{3}h=20min\)

20 phút