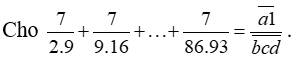\(\dfrac{-3}{4}< \dfrac{a}{12}< \dfrac{-5}{9}\)

\(\Rightarrow\dfrac{-27}{36}< \dfrac{3a}{36}< \dfrac{-20}{36}\)

\(\Rightarrow-27< 3a< -20\)

\(\Rightarrow a=\left\{-8;-7\right\}\)

\(9:27^x=\dfrac{1}{18}\)

\(\Rightarrow9:\left(3^3\right)^x=\dfrac{1}{18}\)

\(\Rightarrow3^{3x}=9:\dfrac{1}{18}\)

\(\Rightarrow3^{3x}=162\)

Xem lại đề 

\(\dfrac{7}{2\cdot9}+\dfrac{7}{9\cdot16}+....+\dfrac{7}{86\cdot93}=\dfrac{\overline{a1}}{\overline{bcd}}\)

\(\Rightarrow\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{86}-\dfrac{1}{93}=\dfrac{\overline{a1}}{\overline{bcd}}\)

\(\Rightarrow\dfrac{1}{2}-\left(\dfrac{1}{9}-\dfrac{1}{9}\right)-\left(\dfrac{1}{16}-\dfrac{1}{16}\right)-...-\left(\dfrac{1}{86}-\dfrac{1}{86}\right)-\dfrac{1}{93}=\dfrac{\overline{a1}}{\overline{bcd}}\)

\(\Rightarrow\dfrac{1}{2}-\dfrac{1}{93}=\dfrac{\overline{a1}}{\overline{bcd}}\)

\(\Rightarrow\dfrac{91}{186}=\dfrac{\overline{a1}}{\overline{bcd}}\)

(1): \(\overline{a1}=91\Rightarrow a=9\)

(2): \(\overline{bcd}=186\Rightarrow\left\{{}\begin{matrix}b=1\\c=8\\d=6\end{matrix}\right.\)

Vậy: ... 

\(v_1=18km/h=5m/s\)

Quãng đường xe thứ nhất đi: \(S_1=5\cdot24=120\left(m\right)\)

Hai xe đi ngược chiều, quãng đường xe thứ nhất đi: 

\(S_1=480-24v_2\left(m\right)\)

Hai xe gặp nhau \(\Leftrightarrow S_1=S_2\)

\(\Rightarrow480-24v_2=120\Rightarrow v_2=15m/s\)

em đổi lại \(t=24s\) thì hai xe đuổi kịp nhau

Như vậy bài toán mới hợp lí

Một số thành tựu văn hóa Ấn Độ:

– Tôn giáo: đạo Hindu, , đạo Phật.

– Chữ viết:

+ Phổ biến nhất là chữ Phạn.

+ Chữ Phạn là nguồn gốc của chữ Hindu thông dụng  ở Ấn Độ.

– Văn học – nghệ thuật:

+ Hàng loạt tác phẩm chính luận, sử thi, kịch thơ,…

+ Hai bộ sử thi Ma-ha-bha-ra-ta và Ra-ma-ya-na. Thời Gúp-ta có Ka-li-đa-sa – ngôi sao sân khấu và văn học Ấn Độ, tác giả nhiều vở kịch nổi tiếng.

– Kiến trúc, điêu khắc:

+ Chịu ảnh hưởng sâu sắc của tôn giáo.

+ Nhiều công trình kiến trúc đền thờ, chùa mang phong cách tôn giáo.

Đây là một số gợi ý của tớ nhé ! cậu dựa vào để viết bài nhé!

\(\left|5x\right|-3x=2\)

\(\text{⇒}\left|5x\right|=3x+2\)  

TH1: 

\(5x=3x+2\) \(\left(x\ge0\right)\)

\(\text{⇒}5x-3x=2\)

\(\text{⇒}2x=2\)

\(\text{⇒}x=\dfrac{2}{2}\)

\(\text{⇒}x=1\left(tm\right)\)

TH2: 

\(-5x=3x+2\) (x < 0) 

\(\text{⇒}-5x-3x=2\)

\(\text{⇒}-8x=2\)

\(\text{⇒}x=-\dfrac{1}{4}\left(tm\right)\)

Xét \(x>0\)

\(5x-3x=2\)

\(\left(5-3\right)x=2\)

\(2x=2\)

\(x=1\)

Xét \(x< 0\)

\(\left(-5x\right)-3x=2\)

\(\left(-5-3\right)x=2\)

\(-8x=2\)

\(x=-\dfrac{2}{8}=-\dfrac{1}{4}\)

Vậy: \(\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{4}\end{matrix}\right.\)

Ta viết lại tổng này thành:

\(P=\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{97.99}\right)+\left(\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{98.100}\right)-\dfrac{49}{99}\)

\(P=\dfrac{1}{2}.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{97.99}\right)+\dfrac{1}{2}\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{98.100}-\dfrac{49}{99}\right)\)

\(P=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{98}-\dfrac{1}{100}\right)-\dfrac{49}{99}\)

\(P=\dfrac{1}{2}\left(1-\dfrac{1}{99}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{100}\right)-\dfrac{49}{99}\)

\(P=\dfrac{1}{2}-\dfrac{1}{198}+\dfrac{1}{4}-\dfrac{1}{200}-\dfrac{49}{99}\)

\(P=\dfrac{49}{200}\)