(x + 2)^2 - y^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
b: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>MN=AH
Xét ΔAMH vuông tại M và ΔAHB vuông tại H có
\(\widehat{MAH}\) chung
Do đó: ΔAMH~ΔAHB
=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AM\cdot AB=MN^2\)
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH~ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AN\cdot AC=MN^2\)
\(AM\cdot AB+AN\cdot AC=MN^2+MN^2=2MN^2\)
c: Ta có: \(\widehat{KAN}+\widehat{ANM}=90^0\)(AK\(\perp\)MN)
mà \(\widehat{ANM}=\widehat{B}\left(=\widehat{AHM}\right)\)
nên \(\widehat{KAN}+\widehat{B}=90^0\)
mà \(\widehat{B}+\widehat{C}=90^0\)
nên \(\widehat{KAC}=\widehat{KCA}\)
=>KA=KC
Ta có: \(\widehat{KAC}+\widehat{KAB}=90^0\)
\(\widehat{KCA}+\widehat{KBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{KAC}=\widehat{KCA}\)
nên \(\widehat{KAB}=\widehat{KBA}\)
=>KA=KB
mà KA=KC
nên KB=KC
=>K là trung điểm của BC


1)
Gọi CTHH của X là \(Al_xCl_y\)
Theo đề có:
\(\%m_{Al}=\dfrac{27x.100\%}{133,5}=20,225\%\Rightarrow x=1\)
\(\Rightarrow y=\dfrac{133,5-27.1}{35,5}=3\)
=> CTHH X: \(AlCl_3\)
2)
\(n_{CO_2}=\dfrac{336:1000}{24,79}=0,014\left(mol\right)\)
\(C+O_2\underrightarrow{t^o}CO_2\)
\(m_{O_2}=0,014.32=0,434\left(g\right)\\ m_C=0,014.12=0,168\left(g\right)\)

Xét tứ giác MNPQ ta có:
\(\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360^o\) (tổng các góc trong tam giác)\
\(\widehat{M}:\widehat{N}:\widehat{P}:\widehat{Q}=1:2:3:4\\ =>\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{\widehat{M}}{1}=\dfrac{\widehat{N}}{2}=\dfrac{\widehat{P}}{3}=\dfrac{\widehat{Q}}{4}=\dfrac{\widehat{M}+\widehat{N}+\widehat{Q}+\widehat{Q}}{1+2+3+4}=\dfrac{360^o}{10}=36^o\\ =>\widehat{M}=36^o\\ =>\dfrac{\widehat{N}}{2}=36^o=>\widehat{N}=72^o\\ =>\dfrac{\widehat{P}}{3}=36^o=>\widehat{P}=108^o\\ =>\dfrac{\widehat{Q}}{4}=36^o=>\widehat{Q}=144^o\)
Vì: \(\widehat{M}+\widehat{Q}=36^o+144^o=180^o\) => MN//PQ => MNPQ là hình thang

\(a,A=x^2+y^2+2x-6y-2\\ =\left(x^2+2x+1\right)+\left(y^2-6y+9\right)-12\\ =\left(x+1\right)^2+\left(y-3\right)^2-12\)
Ta có:
`(x+1)^2>=0` với mọi x
`(y-3)^2>=0` với mọi y
`=>A=(x+1)^2+(y-3)^2-12>=-12` với mọi x,y
Dấu "=" xảy ra: `x+1=0` và `y-3=0`
`<=>x=-1` và `y=3`
\(b,B=5x^2+y^2+z^2+4xy+2xz\\ =\left(4x^2+4xy+y^2\right)+\left(x^2+2xz+z^2\right)\\ =\left(2x+y\right)^2+\left(x+z\right)^2\)
Ta có:
`(2x+y)^2>=0` với mọi x,y
`(x+z)^2>=0` với mọi x,z
`=>B=(2x+y)^2+(x+z)^2>=0`
Dấu "=" xảy ra: `2x+y=0` và `x+z=0`
`<=>2x=-y=-2z`
\(c,C=2x^2+y^2+2xy-8x+2024\\ =\left(x^2+2xy+y^2\right)+\left(x^2-8x+16\right)+2008\\ =\left(x+y\right)^2+\left(x-4\right)^2+2008\)
Ta có:
`(x+y)^2>=0` với mọi x,y
`(x-4)^2>=0` với mọi x
`=>C=(x+y)^2+(x-4)^2+2008>=2008`
Dấu "=" xảy ra:
`x+y=0` và `x-4=0`
`<=>x=4` và `y=-4`
\(d,D=x^2-2xy+3y^2-2x+1997\\ =\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-2y+\dfrac{1}{2}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{3991}{2}\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-1/2)^2>=0` với mọi y
`=>D=(-x+y+1)^2+2(y-1/2)^2+3991/2>=3991/2`
Dấu "=" xảy ra: `-x+y+1=0` và `y-1/2=0`
`<=>y=1/2` và `x=3/2`

ΔEHF vuông tại H
=>\(HE^2+HF^2=EF^2\)
=>\(HE=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔHEG vuông tại H và ΔHFE vuông tại H có
\(\widehat{HEG}=\widehat{HFE}\left(=90^0-\widehat{G}\right)\)
Do đó: ΔHEG~ΔHFE
=>\(\dfrac{HE}{HF}=\dfrac{HG}{HE}\)
=>\(HE^2=HF\cdot HG\)
=>\(HG=\dfrac{4^2}{3}=\dfrac{16}{3}\left(cm\right)\)
ΔEHG vuông tại H
=>\(HE^2+HG^2=EG^2\)
=>\(EG=\sqrt{\left(\dfrac{16}{3}\right)^2+4^2}=\dfrac{8\sqrt{13}}{3}\left(cm\right)\)



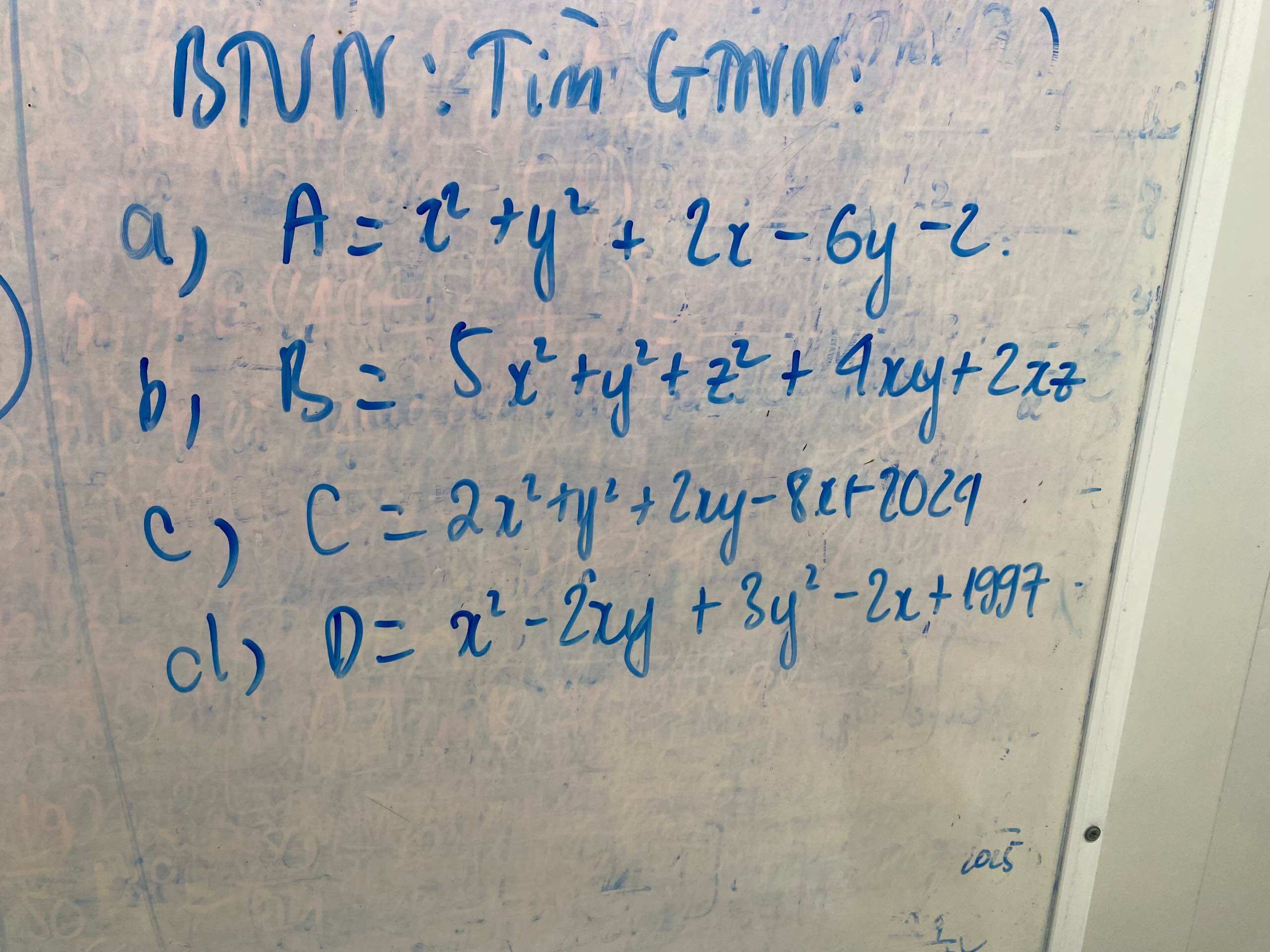
Đề yêu cầu cái gì thế? Em ơi!
????????