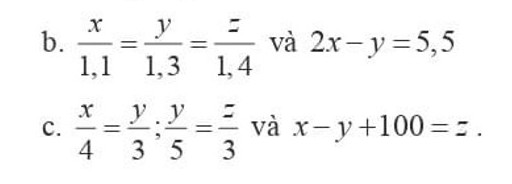Giải:

15.4 = 12.5

ta có các tỉ lệ thức:

a; \(\frac{15}{12}\) = \(\frac54\); b; \(\frac{15}{5}\) = \(\frac{12}{4}\); \(\frac{4}{12}\) = \(\frac{5}{15}\); \(\frac45\) = \(\frac{12}{15}\)

Các tỉ lệ thức có thể lập:

\(\dfrac{15}{12}=\dfrac{5}{4}\)

\(\dfrac{15}{5}=\dfrac{12}{4}\)

\(\dfrac{12}{15}=\dfrac{4}{5}\)

\(\dfrac{5}{15}=\dfrac{4}{12}\)

ĐKXĐ: x<>0

\(\dfrac{-1}{x}=\dfrac{-x}{9}\)

=>\(\dfrac{1}{x}=\dfrac{x}{9}\)

=>\(x\cdot x=1\cdot9\)

=>\(x^2=9\)

=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)

Olm chào em, hiện tại câu hỏi của em chưa hiển thị đấy có thể là do file mà em tải lên bị lỗi nên đã không hiển thị trên diễn đàn. Em nên viết đề bài trực tiếp trên Olm. Như vậy em sẽ không mắc phải lỗi file đề. Điều này giúp em nhanh chóng nhận được sự trợ giúp từ cộng đồng olm. Cảm ơn em đã đồng hành cùng Olm.

Số người của đội sau khi có thêm 3 người nữa là:

12+3=15(người)

Thời gian hoàn thành công việc là:

\(12\cdot\dfrac{10}{15}=12\cdot\dfrac{2}{3}=8\left(giờ\right)\)

Giải:

Một người sẽ hoàn thành công việc sau: 10 x 12 = 120 (giờ)

Thực tế số người làm công việc đó là: 12 + 3 = 15 (người)

Thời gian để hoàn thành công việc đó với 15 người là:

120 : 15 = 8 (giờ)

Kết luận: 10 người sẽ hoàn thành công việc sau 8 giờ

3\(x\) = 5y; \(x+y=40\)

3\(x\) = 5y suy ra: \(x=\frac53\)y thay vào \(x+y=40\) ta được:

\(\frac53y+y=40\)

8y = 120

y = \(\frac{120}{8}\)

y = 15 thay vào \(x=\frac53y\) ta được \(x=\) \(\frac53\times15=25\)

Vậy (\(x;y\) ) = (25; 15)

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{1,1}=\dfrac{y}{1,3}=\dfrac{z}{1,4}=\dfrac{2x-y}{2\cdot1,1-1,3}=\dfrac{5.5}{0.9}=\dfrac{55}{9}\)

=>\(\left\{{}\begin{matrix}x=\dfrac{55}{9}\cdot1,1=\dfrac{121}{18}\\y=\dfrac{55}{9}\cdot1,3=\dfrac{143}{18}\\z=\dfrac{55}{9}\cdot1,4=\dfrac{77}{9}\end{matrix}\right.\)

c:

x-y+100=z

=>x-y-z=-100

 \(\dfrac{x}{4}=\dfrac{y}{3}\)

=>\(\dfrac{x}{20}=\dfrac{y}{15}\left(1\right)\)

\(\dfrac{y}{5}=\dfrac{z}{3}\)

=>\(\dfrac{y}{15}=\dfrac{z}{9}\left(2\right)\)

Từ (1),(2) suy ra \(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{9}\)

mà x-y-z=-100

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{9}=\dfrac{x-y-z}{20-15-9}=\dfrac{-100}{-4}=25\)

=>\(\left\{{}\begin{matrix}x=25\cdot20=500\\y=25\cdot15=375\\z=25\cdot9=225\end{matrix}\right.\)

em cảm ơn ạ

Để xác định hướng của đường sức từ, bạn có thể sử dụng các phương pháp sau: 1. Quy tắc nắm tay phải (đối với dòng điện thẳng hoặc cuộn dây): Dòng điện thẳng: Nắm tay phải sao cho ngón cái chỉ theo chiều dòng điện. Các ngón tay còn lại cuốn quanh dây dẫn sẽ chỉ hướng của đường sức từ xung quanh dây. Cuộn dây (solenoid): Nắm tay phải sao cho các ngón tay cuốn theo chiều dòng điện chạy qua các vòng dây. Ngón cái duỗi thẳng sẽ chỉ hướng của đường sức từ bên trong cuộn dây. 2. Kim nam châm thử: Đặt một kim nam châm nhỏ gần nguồn từ trường (ví dụ, nam châm hoặc dây dẫn có dòng điện). Đầu kim chỉ cực Bắc của kim nam châm sẽ chỉ theo hướng của đường sức từ tại điểm đó. Đường sức từ đi ra từ cực Bắc của nam châm và quay về cực Nam. 3. Quy tắc tay phải (đối với lực từ): Đặt bàn tay phải sao cho ngón cái chỉ theo chiều dòng điện, các ngón tay khác chỉ theo chiều đường sức từ (từ Bắc sang Nam). Lòng bàn tay sẽ chỉ hướng của lực từ tác động lên dòng điện. 4. Sử dụng bột sắt: Rắc bột sắt xung quanh một nam châm. Các hạt sắt sẽ xếp thành các đường sức từ, cho thấy hướng của chúng (từ cực Bắc đến cực Nam). Những phương pháp này giúp xác định hướng và hình dạng của đường sức từ trong các trường hợp khác nhau.

a: 2y=3z

=>\(\dfrac{y}{3}=\dfrac{z}{2}\)

=>\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{2}\)

mà x+y+z=49

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{2}=\dfrac{x+y+z}{2+3+2}=\dfrac{49}{7}=7\)

=>\(\left\{{}\begin{matrix}x=7\cdot2=14\\y=7\cdot3=21\\z=7\cdot2=14\end{matrix}\right.\)

b: 5y=3z

=>\(\dfrac{y}{3}=\dfrac{z}{5}\)

=>\(\dfrac{y}{15}=\dfrac{z}{25}\left(3\right)\)

\(\dfrac{x}{3}=\dfrac{y}{5}\)

=>\(\dfrac{x}{9}=\dfrac{y}{15}\left(4\right)\)

Từ (3),(4) suy ra \(\dfrac{x}{9}=\dfrac{y}{15}=\dfrac{z}{25}\)

mà x+y+z=98

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{9}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{9+15+25}=\dfrac{98}{49}=2\)

=>\(\left\{{}\begin{matrix}x=2\cdot9=18\\y=2\cdot15=30\\z=2\cdot25=50\end{matrix}\right.\)

c: 7y=5z

=>\(\dfrac{y}{5}=\dfrac{z}{7}\)

=>\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)

mà x-y+z=45

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x-y+z}{3-5+7}=\dfrac{45}{5}=9\)

=>\(\left\{{}\begin{matrix}x=9\cdot3=27\\y=9\cdot5=45\\z=9\cdot7=63\end{matrix}\right.\)

d: 2x=3y

=>\(\dfrac{x}{3}=\dfrac{y}{2}\)

=>\(\dfrac{x}{9}=\dfrac{y}{6}\left(1\right)\)

\(\dfrac{y}{3}=\dfrac{z}{2}\)

=>\(\dfrac{y}{6}=\dfrac{z}{4}\left(2\right)\)

Từ (1),(2) suy ra \(\dfrac{x}{9}=\dfrac{y}{6}=\dfrac{z}{4}\)

mà x+y-z=21

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{9}=\dfrac{y}{6}=\dfrac{z}{4}=\dfrac{x+y-z}{9+6-4}=\dfrac{21}{11}\)

=>\(\left\{{}\begin{matrix}x=\dfrac{21}{11}\cdot9=\dfrac{189}{11}\\y=\dfrac{21}{11}\cdot6=\dfrac{126}{11}\\z=\dfrac{21}{11}\cdot4=\dfrac{84}{11}\end{matrix}\right.\)