
Lập bản vẽ kĩ thuật của vật thể giá chữ $U$ được biểu diễn trên giấy kẻ ô tam giác đều trong hình vẽ. Quy ước mỗi cạnh của tam giác đều có chiều dài là $1$ cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

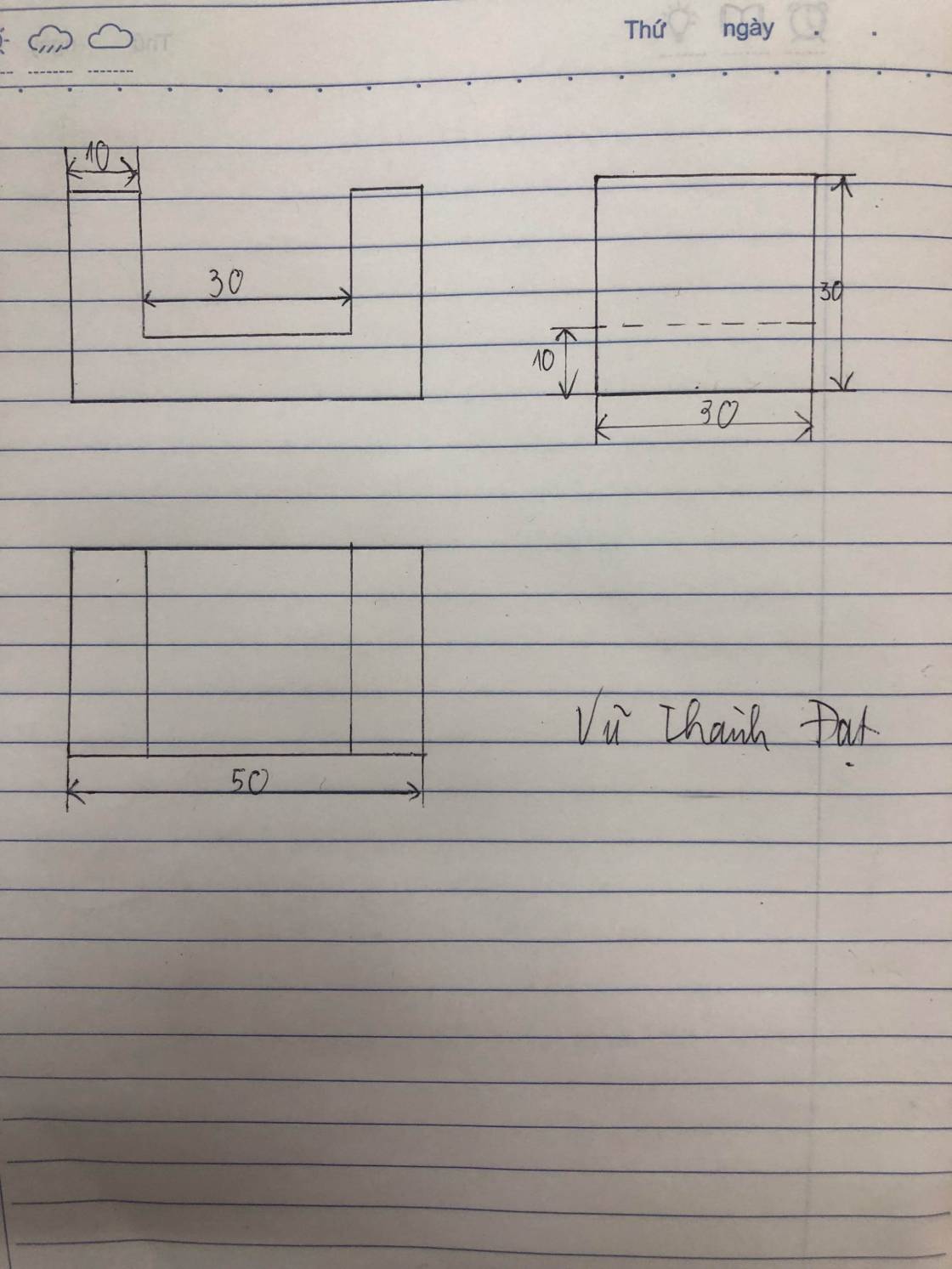
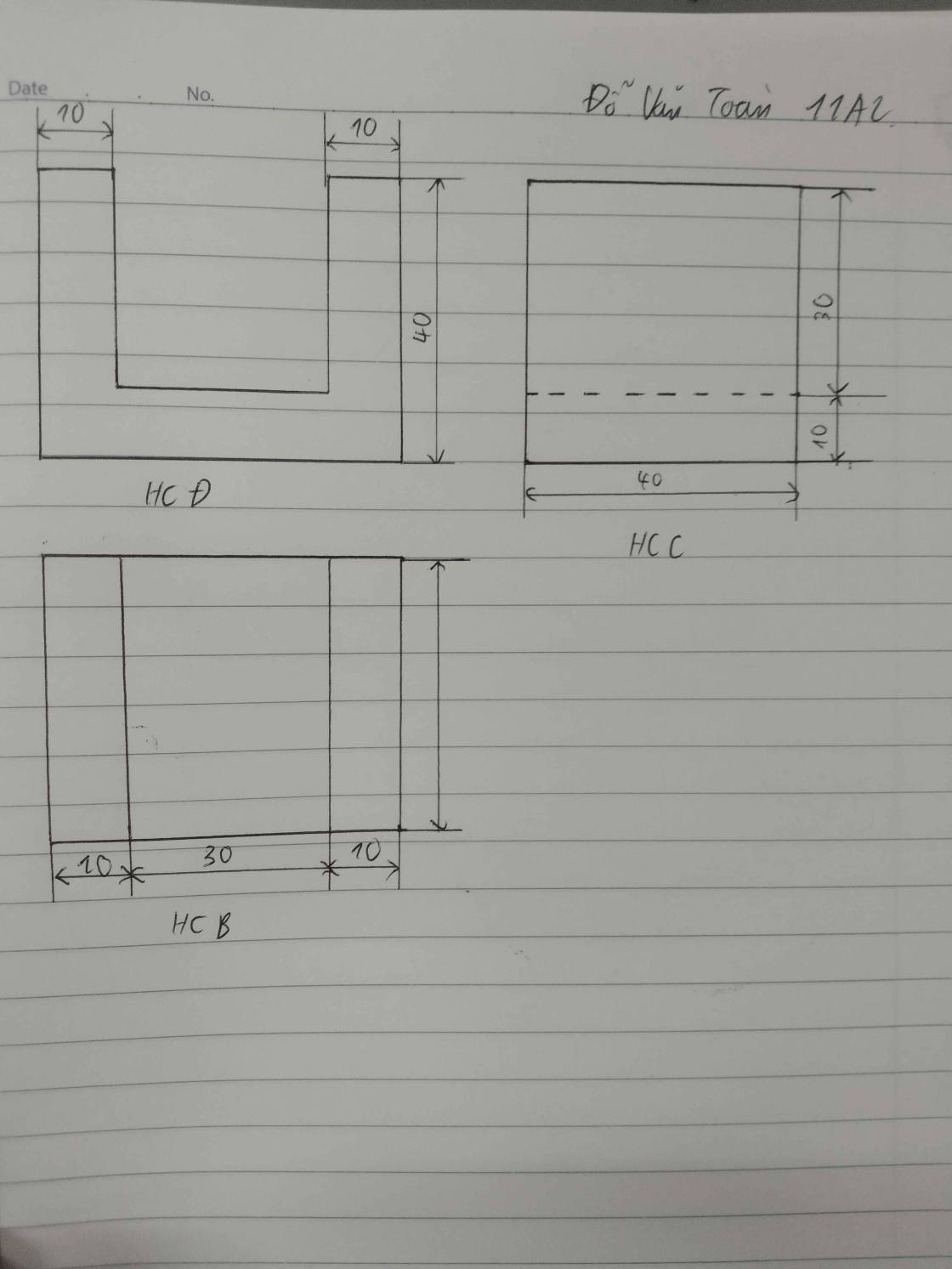

Bản vẽ được thể hiện trong hình vẽ không đáp ứng được nguyên tắc đầy đủ về kĩ thuật là vì bản vẽ thiếu một kích thước nên không thể xác định cụ thể hình ảnh của vật và bản vẽ không có hình khối (3D) mô phỏng hình ảnh của vật
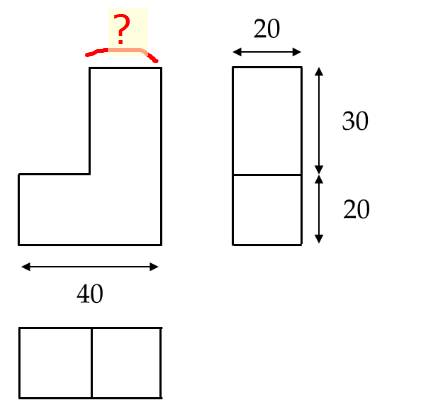
Kích thước bị thiếu là:

Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.

Rất rõ ràng là câu A nhé bạn, vì \(O\in AC\subset\left(SAC\right)\)

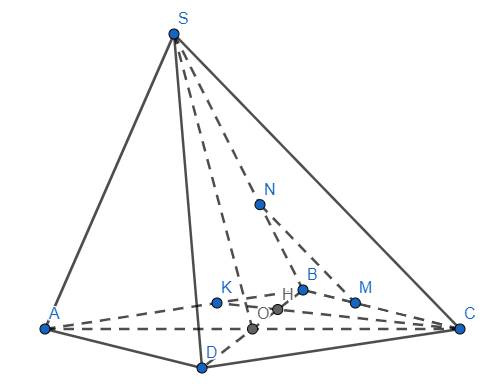
a) Ta có \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\S\subset\left(SBD\right)\end{matrix}\right.\)
và \(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\) nên SO chính là giao tuyến của (SAC) và (SBD)
b) Trong mp(ABCD) cho CK cắt BD tại H. Do \(BD\subset\left(SBD\right)\) nên H cũng là giao điểm của CK và (SBD).
c) Vì \(\dfrac{BN}{NS}=\dfrac{BM}{MC}=\dfrac{1}{2}\) \(\Rightarrow\) MN//SC (Thelas đảo)
\(\Rightarrow\) MN//(SAC)