D = \(\dfrac{1}{2.7}\) + \(\dfrac{1}{7.12}\) + \(\dfrac{1}{12.17}\) + ... + \(\dfrac{1}{37.42}\)

D = \(\dfrac{5}{5}\).(\(\dfrac{1}{2.7}\) + \(\dfrac{1}{7.12}\)+ \(\dfrac{1}{12.17}\)+...+ \(\dfrac{1}{37.42}\))

D = \(\dfrac{1}{5}\).\(\left(\dfrac{5}{2.7}+\dfrac{5}{7.12}+\dfrac{5}{12.17}+...+\dfrac{5}{37.42}\right)\)

D = \(\dfrac{1}{5}\).(\(\dfrac{1}{2}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{12}\) + \(\dfrac{1}{12}\) - \(\dfrac{1}{17}\) + ... + \(\dfrac{1}{37}\) - \(\dfrac{1}{42}\))

D = \(\dfrac{1}{5}\).( \(\dfrac{1}{2}\) - \(\dfrac{1}{42}\))

D = \(\dfrac{1}{5}\) . \(\dfrac{10}{21}\)

D = \(\dfrac{2}{21}\)

\(D=\dfrac{1}{2.7}+\dfrac{1}{7.12}+\dfrac{1}{12.17}+...+\dfrac{1}{37.42}\)

\(=\dfrac{1}{5}.\left(\dfrac{7-2}{2.7}+\dfrac{12-7}{7.12}+\dfrac{17-12}{12.17}+...+\dfrac{42-37}{37.42}\right)\)

\(=\dfrac{1}{5}.\left(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{17}+...+\dfrac{1}{37}-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{5}.\left(\dfrac{1}{2}-\dfrac{1}{42}\right)\)

\(=\dfrac{1}{5}.\dfrac{10}{21}\)

\(=\dfrac{2}{21}\)

\(3+\dfrac{7}{6}=4+\dfrac{1}{6}=\dfrac{25}{6}\)

S

1 giờ 30 phút = 1,5 giờ

2 giờ 20 phút = \(\dfrac{7}{3}\) giờ

Quãng đường người đó đi với vận tốc 15,5 km/giờ:

\(15,5\times1,5=23,25\left(km\right)\)

Quãng đường người đó đi với vận tốc 12 km/giờ:

\(12\times\dfrac{7}{3}=28\left(km\right)\)

Quãng đường từ Đà Nẵng đến Mỹ Sơn dài:

\(23,25+28=51,25\left(km\right)\)

Đổi đơn vị:

1 giờ 30 phút = 1,5 giờ

2 giờ 20 phút = 2,33 giờ

Quãng đường đi được trong 1,5 giờ đầu:

Quãng đường = Vận tốc x Thời gian

Quãng đường = 15,5km/giờ x 1,5 giờ

Quãng đường = 23,25km

Quãng đường đi được trong 2,33 giờ tiếp theo:

Quãng đường = Vận tốc x Thời gian

Quãng đường = 12km/giờ x 2,33 giờ

Quãng đường = 27,96km

Quãng đường từ Đà Nẵng đến Mỹ Sơn:

Quãng đường = Quãng đường đi được trong 1,5 giờ đầu + Quãng đường đi được trong 2,33 giờ tiếp theo

Quãng đường = 23,25km + 27,96km

Quãng đường = 51,21km

\(\dfrac{2^{19}.27^3+15.4^9.9^4}{9^4.4^{10}.12^{10}}\)

\(=\dfrac{2^{19}.\left(3^3\right)^3+3.5.\left(2^2\right)^9.\left(3^2\right)^4}{\left(3^2\right)^4.\left(2^2\right)^{10}.\left(2^2.3\right)^{10}}\)

\(=\dfrac{2^{19}.3^9+3.5.2^{18}.3^8}{3^8.2^{20}.2^{20}.3^{10}}\)

\(=\dfrac{2^{19}.3^9+3^9.5.2^{18}}{3^{18}.2^{40}}\)

\(=\dfrac{2^{18}.3^9.\left(2+5\right)}{3^{18}.2^{40}}\)

\(=\dfrac{7}{3^9.2^{22}}\)

2 19 . 2 7 3 + 15. 4 9 . 9 4 9 4 . 4 10 + 1 2 10 9 4 .4 10 +12 10

2 19 .( 2 7 3 + 27 3 ) + 15.4 9 .( 9 4 9 4 + 9 4 ) + 1 2 10 9 4 .4 10 +12 10

= 2 19 .100 + 15.4 9 . 94 + 1 2 10 9 4 .4 10 +12 10

= 2000 + 1410 + 1 2 10 9 4 .4 10 +12 10

= 2000 + 1410 + 2 10 9 + 12 10

3424

Quy đổi đơn vị:

1 giờ = 60 phút = 3600 giây

Giải:

Gọi vận tốc của người thứ nhất là x km/h (x > 0).

Khi đó, vân tốc của người thứ hai là x + 14 km/h.

Thời gian người thứ nhất đi từ A đến B là: 8 giờ - 6 giờ = 2 giờ.

Thời gian người thứ hai đi từ A đến B là: 11 giờ - 8 giờ = 3 giờ.

Quãng đường từ A đến B là:

• Người thứ nhất: 2x km
• Người thứ hai: 3(x + 14) km

Vì quãng đường từ A đến B là như nhau nên ta có phương trình:

2x = 3(x + 14)

Giải phương trình:

2x = 3x + 42 => x = 42

Vậy vận tốc của người thứ nhất là 42 km/h, vận tốc của người thứ hai là 42 + 14 = 56 km/h.

Tính hợp lý:

Chứng minh định lý:

Kẻ AH vuông góc với BC.

Ta có:

• ΔADE và ΔADH có:

  • Góc ADE = Góc ADH (= 90 độ)
  • AD chung
  • Góc DAE = Góc HAD (cùng phụ với góc EAD) => ΔADE ~ ΔADH (g-g) => DE/DH = AD/AE (1)

• ΔCDG và ΔCDH có:

  • Góc CDG = Góc CDH (= 90 độ)
  • CD chung
  • Góc DGC = Góc HDG (cùng phụ với góc CDG) => ΔCDG ~ ΔCDH (g-g) => DG/DH = CD/CE (2)

Nhân (1) và (2), ta được:

DE/DH . DG/DH = AD/AE . CD/CE => DE . DG = AD . CD

Vậy DB . DC = DE . DG (đpcm)

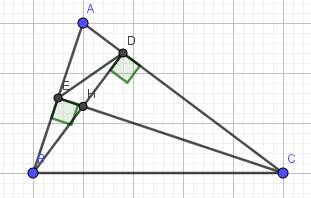
a) Xét hai tam giác vuông: \(\Delta ABD\) và \(\Delta ACE\) có:

\(\widehat{A}\) chung

\(\Rightarrow\Delta ABD\) ∽ \(\Delta ACE\left(g-g\right)\)

\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\)

\(\Rightarrow AE.AB=AD.AC\)

b) Do \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\left(cmt\right)\)

\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

Xét \(\Delta ADE\) và \(\Delta ABC\) có:

\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(cmt\right)\)

\(\widehat{A}\) chung

\(\Rightarrow\Delta ADE\) ∽ \(\Delta ABC\left(g-g\right)\)

\(\Rightarrow\widehat{ADE}=\widehat{ABC}\)

Sau mỗi bước, Đông xóa hai số a và b và viết lên bảng a + b.

Do đó tổng các số trên bảng không thay đổi.

Khi đó ta suy ra số cuối cùng được viết trên bảng là tổng các số trên bảng lúc đầu.

Vậy số cuối cùng là:

(15 + 1).16 : 2 = 128 số

Hai bố con Việt cùng về quê bằng xe máy. Việt khởi hành lúc 5 giờ sáng. Bố của Việt khởi hành lúc 6 h sáng với vận tốc nhanh hơn vận tốc của Viêt là 10km/h và cả hai cùng đến quê lúc 10 giờ. Tính quãng đường từ nhà Việt về đến quê. Biết cả hai bố con cùng đi trên 1 cung đường.