Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi 3 cạnh tam giác lần lượt là x,y,z ( x,y,z khác 0)
Theo đề bài, ta có:
x:y:z = 3:5:7 = x/3 = y/5 = z/7 = x+y+z/3+5+7 = 245/15 = 49/3
suy ra x là cạnh 1 sẽ bằng 49
y là cạnh 2 sẽ bằng 245/3
z là cạnh 3 sẽ bằng 343/3

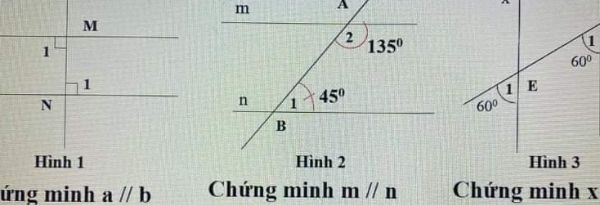
a) Định lí : 1 đường thẳng vuông góc với 2 đường thẳng thì 2 đường thẳng đó song song
b) 2 góc cùng phía bù nhau thì hai đường thẳng song song
c) 2 góc đồng vị bằng nhau thì hai đường thẳng song song

Tiên đề trong toán học
Nổi tiếng nhất là định đề V của tiên đề Euclid. Nội dung của định đề này là: Nếu hai đường thẳng tạo với một đường thẳng thứ ba hai góc trong cùng phía có tổng nhỏ hơn 180o thì chúng sẽ cắt nhau về phía đó.

\(A=\frac{3}{11.16}+\frac{3}{16.21}+\frac{3}{21.26}+....+\frac{3}{61.66}\)
\(A=\frac{3}{5}\left[\left(\frac{1}{11}-\frac{1}{16}\right)+\left(\frac{1}{16}-\frac{1}{21}\right)+\left(\frac{1}{21}-\frac{1}{26}\right)+....+\left(\frac{1}{61}-\frac{1}{66}\right)\right]\)
\(A=\frac{3}{5}\left(\frac{1}{11}-\frac{1}{16}+\frac{1}{16}-\frac{1}{21}+...+\frac{1}{61}-\frac{1}{66}\right)\)
\(A=\frac{3}{5}\left(\frac{1}{11}-\frac{1}{66}\right)\)
\(A=\frac{3}{5}.\frac{5}{66}\)
\(A=\frac{1}{22}\)

Đáp án:
a) Nếu a+b là số vô tỉ thì bb có thể là số vô tỉ hoặc hữu tỉ
b) Nếu a.b là số hữu tỉ thì b là số vô tỉ


\(\frac{x+1}{3}=\frac{y+2}{-4}=\frac{z-3}{5}=\frac{5x+5}{15}=\frac{y+2}{-4}=\frac{2z-6}{10}=\)
\(=\frac{\left(5x+y+2z\right)+1}{21}=\frac{41+1}{21}=2\)
\(\Rightarrow\frac{x+1}{3}=2\Rightarrow x=5;\frac{y+2}{-4}=2\Rightarrow y=-10;\frac{z-3}{5}=2\Rightarrow z=13\)

 h nhé
h nhé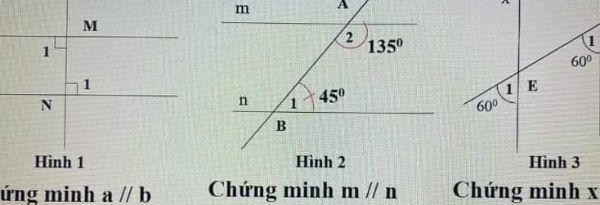

\(C=6^{2002}=\overline{...6}\)( các số tận cùng là 6 nhân với nhau tận cùng cũng là 6 )
\(D=2^{2001}=\left(2^4\right)^{500}.2=\overline{...6}.2=\overline{...2}\) ( vì 2 mũ 4 có tận cùng là 6 )