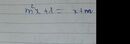Tính diện tích ngũ giác ABCDE có AB=BC=DE=CD+EA=m và góc A =góc C=90 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>AH=ED
b: Xet tứ giác AHEK có
HE//AK
HE=AK
=>AHEK là hình bình hành
tôi chỉ chứng minh k là giao điểm 2 đường truyng tuyến rồi suy ra k là trọng tâm tam giác có được ko



Phân tích đa thức thành nhân tử
a) 2( x + 1 ) - 3y( x + 1 ) = ( x + 1 )( 2 - 3y )
b) x2 - 5x + 4 = x2 - x - 4x + 4 = x( x - 1 ) - 4( x - 1 ) = ( x - 1 )( x - 4 )
Tìm x
a) x( x - 3 ) + 7x - 21 = 0
<=> x( x - 3 ) + 7( x - 3 ) = 0
<=> ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
b) ( x - 2 )2 + x( 3 - x ) = 6
<=> x2 - 4x + 4 + 3x - x2 = 6
<=> -x + 4 = 6
<=> -x = 2
<=> x = -2
\(A=\frac{x-2}{x}\)và \(B=\frac{x}{x-2}-\frac{2x}{x^2-4}\)( x ≠ 0 ; x ≠ ±3 )
a) Tại x = 23 ( tmđk ) => \(A=\frac{23-2}{23}=\frac{21}{23}\)
b) P = A.B
\(=\frac{x-2}{x}\times\left(\frac{x}{x-2}-\frac{2x}{x^2-4}\right)\)
\(=\frac{x-2}{x}\times\left(\frac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{2x}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\frac{x-2}{x}\times\frac{x^2+2x-2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{1}{x}\times\frac{x^2}{x+2}=\frac{x}{x+2}\)
Để P = 4 => \(\frac{x}{x+2}=4\)
=> 4( x + 2 ) = x
=> 4x + 8 - x = 0
=> 3x + 8 = 0
=> x = -8/3 ( tmđk )

\(\frac{2x-1}{2x}+\frac{2x}{1-2x}+\frac{1}{4x^2-2x}=\frac{2x-1}{2x}-\frac{2x}{1-2x}+\frac{1}{2x\left(2x-1\right)}\)
\(=\frac{\left(2x-1\right)^2-4x^2+1}{2x\left(2x-1\right)}=\frac{4x^2-4x-4x^2+2}{2x\left(2x-1\right)}\)
\(=\frac{-2\left(2x-1\right)}{2x\left(2x-1\right)}=\frac{-1}{x}\)
\(\frac{2x-1}{2x}+\frac{2x}{1-2x}+\frac{1}{4x^2-2x}\)
\(=\frac{2x-1}{2x}-\frac{2x}{2x-1}+\frac{1}{2x\left(2x-1\right)}\)
\(=\frac{\left(2x-1\right)^2}{2x\left(2x-1\right)}-\frac{4x^2}{2x\left(2x-1\right)}+\frac{1}{2x\left(2x-1\right)}\)
\(=\frac{4x^2-4x+1-4x^2+1}{2x\left(2x-1\right)}\)
\(=\frac{-4x+2}{2x\left(2x-1\right)}=\frac{-2\left(2x-1\right)}{2x\left(2x-1\right)}=-\frac{1}{x}\)