Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.1. Chứng minh rằng: Tứ giác CEHD, nội tiếp .2. Bốn điểm B,C,E,F cùng nằm trên một đường tròn.3. AE.AC = AH.AD; AD.BC = BE.AC.4. H và M đối xứng nhau qua BC.5. Xác định tâm đường tròn nội tiếp tam giác DEF. Bài 2. Cho tam giác cân ABC (AB = AC), các đường...
Đọc tiếp
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
1. Chứng minh rằng: Tứ giác CEHD, nội tiếp .
2. Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. AE.AC = AH.AD; AD.BC = BE.AC.
4. H và M đối xứng nhau qua BC.
5. Xác định tâm đường tròn nội tiếp tam giác DEF.
Bài 2. Cho tam giác cân ABC (AB = AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.
1. Chứng minh tứ giác CEHD nội tiếp .
2. Bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Chứng minh ED = 1/2 BC.
4. Chứng minh DE là tiếp tuyến của đường tròn (O).
5. Tính độ dài DE biết DH = 2 cm, AH = 6 cm.
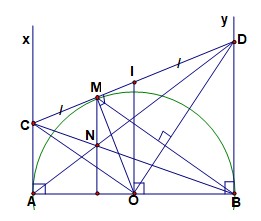
Bài 3. Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax , By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N. Chứng minh:
1. AC + BD = CD
2. Góc COD = 900
3. AC.BD = 1/4 AB2
4. OC // BM
5. AB là tiếp tuyến của đường tròn đường kính CD.
6. MN vuông góc AB.
7. Xác định vị trí của M để chu vi tứ giác ACDB đạt giá trị nhỏ nhất.



Giải thích các bước giải:
1. Cơ thể mang 3 tính trạng trội có kiểu gen như sau:
AABBDD, AaBBDD, AABbDD, AABBDd, AaBbDD, AaBBDd, AABbDd, AaBbDd
2. P: AaBbDd x AabbDd, xét từng cặp gen:
a. Aa x Aa => F1: 1AA : 2 Aa : 1aaa
Bb x bb => F1: 1Bb : 1bb
Dd x Dd => F1: 1DD : 2Dd : 1dd
Số loại kiểu gen ở F1: 3 . 1. 3 = 9
Tỉ lệ KG là: ( 1:2:1)(1:1)(1:2:1)
b. Các cây mang 2 tính trạng trội và 1 tính trạng lặn ở F1 là: A-bbD- , A-B-dd, aaB-D-
Tỉ lệ : . \(\frac{3}{4}\) .\(\frac{1}{2}\).\(\frac{3}{4}\)A-bbD- + \(\frac{1}{2}\). \(\frac{1}{2}\).\(\frac{3}{4}\)A-B-dd + \(\frac{1}{2}\). \(\frac{1}{2}\).\(\frac{3}{4}\)aaB-D- =\(\frac{21}{32}\)
c. TLKH: 3:3:1:1 =( 3:1)(1:1)
=> Vậy P có thể có kiểu gen
AaBbdd x Aabbdd
AaBbdd x AabbDd
AaBbDD x AabbDD
AaBBDd x AaBBdd
AaBBDd x Aabbdd
AabbDd x Aabbdd
AABbDd x AABbdd
AABbDd x aaBbdd
aaBbDd x aaBbdd