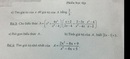

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3=\left(x^2+\frac{1}{x^2}\right)+\left(x^2+\frac{y^2}{4}\right)\ge2+\left|xy\right|\Rightarrow\left|xy\right|\le1\Rightarrow-1\le xy\le1\Rightarrow Bantulmtiep\)
dùng bđt cô si vào phần giả thiết đã cho nhé bạn , mình đang bận không tiện làm . Nếu cần thì tối rảnh mình làm cho

Đổi 5 phút = 300 giây
360kj = 360000j
Quãng đường ngựa đi được là :
\(s=\frac{A}{F}=\frac{360000}{600}=600\left(m\right)\)
Vận tốc con ngựa đi được là:
\(v=\frac{s}{t}=\frac{600}{300}=2\left(m\text{/}s\right)\)
Vậy...
Bài làm
Bài 3
a) \(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2x-4}+\frac{2-3x}{x^3-4x}\cdot\frac{x^2-4}{x-2}\right)\)
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x^2-4\right)}\cdot\frac{x^2-4}{x-2}\right)\)
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x-2\right)}\right)\)
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\left(\frac{x\left(x+2\right)}{2x\left(x-2\right)}+\frac{2\left(2-3x\right)}{2x\left(x-2\right)}\right)\)
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\frac{x^2+2x+4-6x}{2x\left(x-2\right)}\)
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\cdot\frac{x^2-4x+4}{2x\left(x-2\right)}\)
\(A=\left(\frac{x^4-4x^2}{x^2-4}+\frac{4x^2}{x^2-4}\right)\cdot\frac{\left(x-2\right)^2}{2x\left(x-2\right)}\)
\(A=\frac{x^4}{\left(x-2\right)\left(x+2\right)}\cdot\frac{x-2}{2x}\)
\(A=\frac{x^3}{2\left(x+2\right)}\)
Vậy \(A=\frac{x^3}{2\left(x+2\right)}\)
b) Ta có: \(\left|2x-1\right|=3\)
<=> \(\orbr{\begin{cases}2x-1=3\\2x-1=-3\end{cases}}\)<=> \(\orbr{\begin{cases}2x=4\\2x=-2\end{cases}}\)<=> \(\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
*) Với x = 2 thì ta thay x = 2 vào A ta được:
\(A=\frac{2^3}{2\left(2+2\right)}=\frac{8}{8}=1\)
Vậy với x = 2 thì A = 1
*) Với x = -1 thì ta thay x = -2 vào ta, ta được:
\(A=\frac{\left(-1\right)^3}{2\left(-1+2\right)}=\frac{-1}{2}\)
Vậy với x = -1 thì x = -1/2
Bài 2:
a) \(A=\left(\frac{x+2}{x^2+2x+1}-\frac{x-2}{x^2-1}\right):\frac{2x^2+x}{x^3+x^2-x-1}\)
\(A=\left(\frac{x+2}{\left(x+1\right)\left(x+1\right)}-\frac{x-2}{\left(x+1\right)\left(x-1\right)}\right):\frac{2x^2+x}{x^2\left(x+1\right)-\left(x+1\right)}\)
\(A=\left(\frac{\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x+1\right)\left(x-1\right)}-\frac{\left(x-2\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)\left(x+1\right)}\right):\frac{2x^2+x}{\left(x+1\right)\left(x+1\right)\left(x-1\right)}\)
\(A=\left(\frac{x^2+2x-x-2}{\left(x+1\right)^2\left(x-1\right)}-\frac{x^2+x-2x-2}{\left(x+1\right)^2\left(x-1\right)}\right)\cdot\frac{\left(x+1\right)^2\left(x-1\right)}{x\left(2x+1\right)}\)
\(A=\frac{x^2+2x-x-2-x^2-x+2x+2}{\left(x+1\right)^2\left(x-1\right)}\cdot\frac{\left(x+1\right)^2\left(x-1\right)}{x\left(2x+1\right)}\)
\(A=4x-2x\cdot\frac{1}{x\left(2x+1\right)}\)
\(A=\frac{2x\left(2-1\right)}{x\left(2x+1\right)}\)
\(A=\frac{4-2}{2x+1}\)
\(A=\frac{2}{2x+1}\)
Để A xác định
<=> 2x + 1 khác 0
<=> 2x khác -1
<=> x khác -1/2
Vậy x khác -1/2 thì A xác định.
b) Thay x = -3 vào A ta được:
\(A=\frac{2}{2\left(-3\right)+1}=\frac{2}{-6+1}=\frac{2}{-5}\)
Vậy x = -3 thì A = 2/-5
Thay x = 1/4 vào A ta được
\(A=\frac{2}{2\cdot\frac{1}{4}+1}=\frac{2}{\frac{1}{2}+1}=\frac{2}{\frac{3}{2}}=2:\frac{3}{2}=2\cdot\frac{2}{3}=\frac{4}{3}\)
Vậy x = 1/4 thì A = 4/3
Vì x = -1/2 (Không thỏa mãn điều kiện)
Do đó với x = -1/2 thì A không xác định.
c) Để |A| = 3
<=> \(\left|\frac{2}{2x+1}\right|=3\)
<=> \(\orbr{\begin{cases}\frac{2}{2x+1}=3\\\frac{2}{2x+1}=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}6x+3=2\\-6x-3=2\end{cases}\Leftrightarrow}\orbr{\begin{cases}6x=-1\\-6x=5\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-\frac{1}{6}\\x=-\frac{5}{6}\end{cases}}}\)
Vậy x = -1/6 hoặc x = -5/6 thì |A| = 3
\(A=\left(x^2+\frac{4x^2}{x^2-4}\right)\left(\frac{x+2}{2x-4}+\frac{2-3x}{x^3-4}.\frac{x^2-4}{x-2}\right)\)
\(=\left(\frac{x^2\left(x^2-4\right)}{x^2-4}+\frac{4x^2}{x^2-4}\right)\left(\frac{x+2}{2\left(x-2\right)}+\frac{\left(2-3x\right)\left(x^2-4\right)}{x\left(x^2-4\right)\left(x-2\right)}\right)\)
\(=\left(\frac{x^2\left(x^2-4\right)+4x^2}{x^2-4}\right)\left(\frac{x+2}{2\left(x-2\right)}+\frac{2-3x}{x\left(x-2\right)}\right)\)
\(=\left(\frac{x^4-4x^2+4x^2}{x^2-4}\right)\left(\frac{x\left(x+2\right)}{2x\left(x-2\right)}+\frac{2\left(2-3x\right)}{2x\left(x-2\right)}\right)\)
\(=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x^2+2x+4-6x}{2x\left(x-2\right)}\right)=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x^2-4x+4}{2x\left(x-2\right)}\right)\)
\(=\left(\frac{x^4}{x^2-4}\right)\left(\frac{\left(x-2\right)^2}{2x\left(x-2\right)}\right)=\left(\frac{x^4}{x^2-4}\right)\left(\frac{x-2}{2x}\right)=\frac{x^4.\left(x-2\right)}{\left(x^2-4\right)2x}\)
\(=\frac{x^4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)2x}=\frac{x^3}{2\left(x+2\right)}\)
b,Ta có:\(\left|2x-1\right|=3\)
\(\Leftrightarrow2x-1=\pm3\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=3\\2x-1=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)
Với x=2 thì giá trị của A là:\(\frac{2^3}{2\left(2+2\right)}=1\)
Với x=-1 thì giá trị biểu thức là:\(\frac{\left(-1\right)^3}{-2\left(-1+2\right)}=-\frac{1}{2}\)