Cho tam giác \(ABC\) vuông tại \(A\). Trên cạnh \(AC\) lấy điểm \(D\), kẻ \(CE\) vuông góc với \(BD\), \(CE\) cắt \(AB\) tại \(K\). Chứng minh rằng:
\(a\)) Bốn điểm \(A,\) \(B,\) \(C,\) \(E\) cùng thuộc một đường tròn.
\(b\)) \(BC^2=CD\cdot CA+BD\cdot BE\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

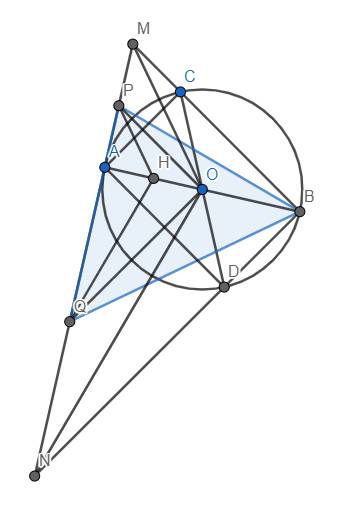
a) Tam giác ABM vuông tại A có đường cao AC nên \(BC.BM=BA^2\). CMTT, \(BD.BN=BA^2\) nên \(BC.BM=BD.BN\Leftrightarrow\dfrac{BM}{BD}=\dfrac{BN}{BC}\). Từ đây dễ dàng suy ra \(\Delta BNM~\Delta BCD\left(c.g.c\right)\) (đpcm)
b) Ta có OQ//BN, OP//BM, mà \(MB\perp NB\) nên suy ra \(OP\perp BN\), từ đó O là trực tâm tam giác BPN.\(\Rightarrow ON\perp BP\)
Lại có \(QH\perp BP\) nên QH//ON.
Tam giác AON có Q là trung điểm AN, QH//ON nên H là trung điểm OA \(\Rightarrow AH=\dfrac{OA}{2}=\dfrac{R}{2}\) không đổi.


Lời giải:
ĐKXĐ: $-1\leq x\leq 1$
PT \(\Rightarrow \left\{\begin{matrix}
x-1\geq 0\\
1-x^2=(x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 1\\
(x-1)^2+(x^2-1)=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x\geq 1\\
(x-1)(x-1+x+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\ge 1\\ 2x(x-1)=0\end{matrix}\right.\Leftrightarrow x=1\)
Vậy ..........

ĐKXĐ:
1 - x² ≥ 0 và x - 1 ≥ 0
⇔ x² ≤ 1 và x ≥ 1
⇔ -1 ≤ x ≤ 1 và x ≥ 1
⇔ x = 1
√1−x2=x−11−�2=�−1
⇔−x2+1=x2−2x+1⇔−�2+1=�2−2�+1
⇔2x2−2x=0⇔2�2−2�=0
⇔x=1

ĐKXĐ:
1 - x² ≥ 0 và x - 1 ≥ 0
⇔ x² ≤ 1 và x ≥ 1
⇔ -1 ≤ x ≤ 1 và x ≥ 1
⇔ x = 1

\(\sqrt{x^2-x}=\sqrt{3-x}\)
ĐK: \(\left\{{}\begin{matrix}x^2-x\ge0\\3-x\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge1\\x\le0\end{matrix}\right.\\x\le3\end{matrix}\right.\) \(\Leftrightarrow x\le3\)
\(\Leftrightarrow x^2-x=3-x\)
\(\Leftrightarrow x^2-x+x=3\)
\(\Leftrightarrow x^2=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\left(tm\right)\)
Vậy: ...

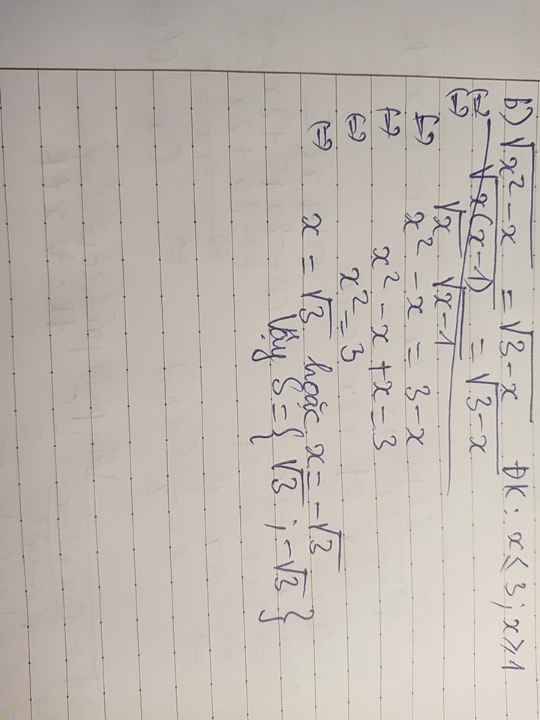
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.