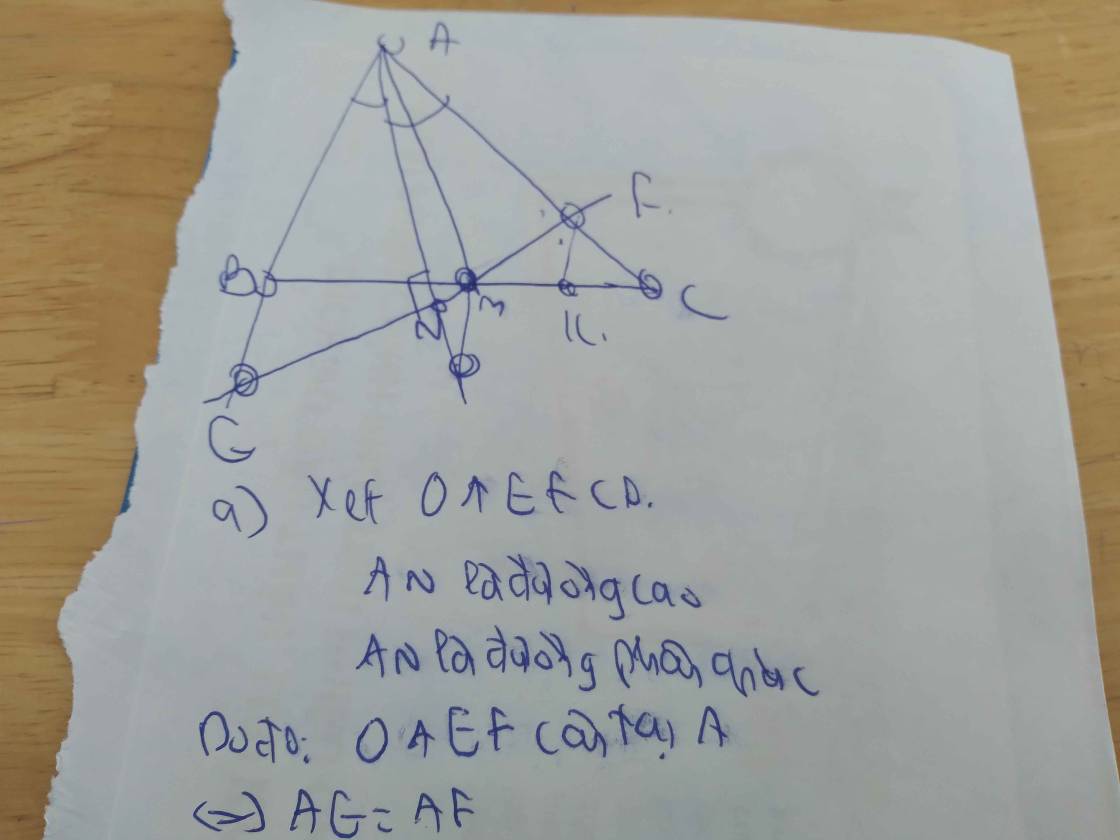
Cho \(\Delta ABC\) có AB<AC. M là trung điểm của BC, từ M kẻ đường thẳng vuông góc với tia phân giác của\(\widehat{A}\), cắt tia này tại N, cắt tia AB tại E và cắt tia AC tại F. Chứng minh rằng:
a, AE=AF
b, BE=CF
c, AE=\(\dfrac{AB+AC}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đôie 7h30p=7.5h ; 15p=1/4h
Minh đi từ nhà tới trường lúc :
7.5-1/4-03=6.95(giờ)
đổi 6.95 giờ =6h57p

a, X x 10/18 + X x 4/9 =19
<=> X x (10/18 + 4/9) =19
<=> X x 1 = 19
<=> X = 1
b, X x 21/9 - X x 1/3 = 28
<=> X x (21/9 - 1/3) = 18
<=> X x 2 = 18
<=> X = 9


\(ab=2\left(a+b\right)\)
\(\Leftrightarrow ab-2a-2b=0\)
\(\Leftrightarrow ab-2a-2b+4=4\)
\(\Leftrightarrow a\left(b-2\right)-2\left(b-2\right)=4\)
\(\Leftrightarrow\left(a-2\right)\left(b-2\right)=4\)
Ta có bảng:
| a-2 | -4 | -2 | -1 | 1 | 2 | 4 |
| b-2 | -1 | -2 | -4 | 4 | 2 | 1 |
| a | -2 | 0 | 1 | 3 | 4 | 6 |
| b | 1 | 0 | -2 | 6 | 4 | 3 |
Do a;b nguyên dương nên \(\left(a;b\right)=\left(3;6\right);\left(4;4\right);\left(6;3\right)\)
ab=2(a+b)
=>ab-2a-2b=0
=>a(b-2)-2b+4=4
=>(a-2)(b-2)=4
=>\(\left(a-2\right)\left(b-2\right)=1\cdot4=4\cdot1=\left(-1\right)\cdot\left(-4\right)=\left(-4\right)\cdot\left(-1\right)=2\cdot2=\left(-2\right)\cdot\left(-2\right)\)
=>\(\left(a-2;b-2\right)\in\left\{\left(1;4\right);\left(4;1\right);\left(-1;-4\right);\left(-4;-1\right);\left(2;2\right);\left(-2;-2\right)\right\}\)
=>\(\left(a;b\right)\in\left\{\left(3;6\right);\left(6;3\right);\left(1;-2\right);\left(-2;1\right);\left(4;4\right);\left(0;0\right)\right\}\)
mà (a;b) là cặp số nguyên dương
nên \(\left(a;b\right)\in\left\{\left(3;6\right);\left(6;3\right);\left(4;4\right)\right\}\)

Chiều cao thửa ruộng hình thang là:
(150 + 50) : 2 = 100 (m)
S thửa ruộng hình thang là:
(150 + 50) x 100 : 2 = 10000(m2)
Cứ 100m2 thu hoạch đc 50 kg thóc thì 10000m2 thu được
10000 : 100 = 100 m2 (=50kg)
Thửa ruộng đó thu hoạch đc là:
100 x 50 = 5000 kg
Đổi 5000kg = 5 tấn
Đ/S: 5 tấn

Số bn đang chơi cầu trượt là:
15x2:5=6(bn)
Đ/S:6bn
Tik cho mikl nha

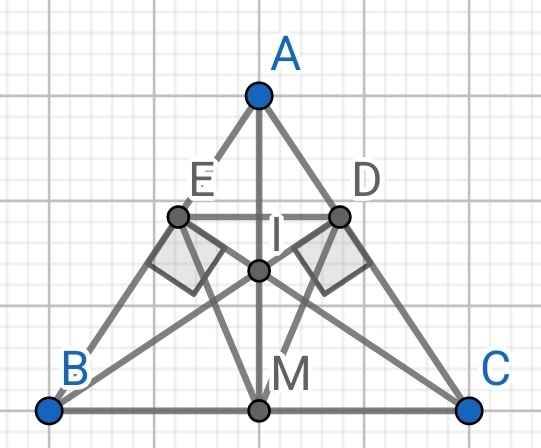
a) Do BD và CE là hai đường cao của ∆ABC (gt)
Mà I là giao điểm của BD và CE (gt)
⇒ AM là đường cao thứ ba của ∆ABC
⇒ AM ⊥ BC
Do ∆ABC cân tại A (gt)
AM là đường cao của ∆ABC (cmt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
b) Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét hai tam giác vuông: ∆ADB và ∆AEC có:
AB = AC (cmt)
∠A chung
⇒ ∆ADB = ∆AEC (cạnh huyền - góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
c) Do AB = AC (cmt)
AE = AB (cmt)
Trừ vế với vế, ta có:
AB - AE = AC - AD
⇒ BE = CD
Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB
⇒ ∠EBM = ∠DCM
Do M là trung điểm của BC (cmt)
⇒ BM = CM
Xét ∆BEM và ∆CDM có:
BE = CD (cmt)
∠EBM = ∠DCM (cmt)
BM = CM (cmt)
⇒ ∆BEM = ∆CDM (c-g-c)
⇒ EM = DM (hai cạnh tương ứng)
∆MED có:
EM = DM (cmt)
⇒ ∆MED cân tại M