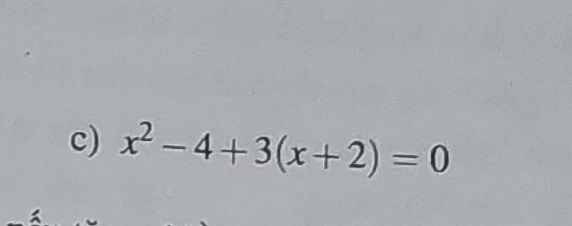
Giải pt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn lấy luôn 2000 : 15=133 (dư 5)
vậy 2000 chữ số 7 chia cho 15 dư 5 nhé!

Lời giải:
Số bị chia gấp 6 lần thương, tức là số chia bằng 6.
Thương là: $1035+6=1041$
Số bị chia là: $1041\times 6=6246$

Trong hai ngày, Na đọc được tổng cộng 42 trang sách. Biết rằng ngày đầu, Na đọc được 1 số trang. Ngày thứ hai, Na đọc được bằng số trang của ngày đầu.
Chúng ta có thể giải bài toán này bằng cách tạo một phương trình. Gọi x là số trang Na đọc được trong ngày đầu. Khi đó, số trang Na đọc được trong ngày thứ hai cũng là x.
Tổng số trang đọc được trong hai ngày là: [ \text{Tổng số trang} = \text{Số trang ngày đầu} + \text{Số trang ngày thứ hai} = x + x = 2x ]
Vì tổng số trang là 42, ta có phương trình: [ 2x = 42 ]
Giải phương trình trên: [ x = \frac{42}{2} = 21 ]
Vậy số trang của cuốn sách đó là 21 trang. 📖

\(\dfrac{320}{24}-\dfrac{100}{8}\\ =\dfrac{40}{3}-\dfrac{25}{2}\\ =\dfrac{80}{6}-\dfrac{75}{6}\\ =\dfrac{5}{6}\)
\(\dfrac{41}{50}+\dfrac{11}{10}\\ =\dfrac{41}{50}+\dfrac{55}{50}\\ =\dfrac{96}{50}=\dfrac{48}{25}\)

Lời giải:
Tổng của phép cộng: $100$
Nếu giữ nguyên số hạng thứ nhất nhưng thêm ở số hạng thứ hai 112 đơn vị thì tổng mới là:
$100+112=212$

a) Ta có:
\(\Delta=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-4m\right)\)
\(=4m^2-8m+4+16m\)
\(=4m^2+8m+4=4\left(m+1\right)^2\ge0\forall m\)
Nên pt luôn có nghiệm
b) Để pt có nghiệm kép thì:
\(\Delta=0\Leftrightarrow4\left(m+1\right)^2=0\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
\(x^2-4+3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)+3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)