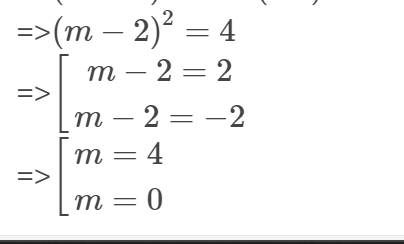Lời giải:

a.

Vì $BE, CF$ là đường cao của tam giác $ABC$ nên $\widehat{BFC}=\widehat{BEC}=90^0$

Tứ giác $BCEF$ có $\widehat{BFC}=\widehat{BEC}$ và cùng nhìn cạnh $BC$ nên $BCEF$ là tứ giác nội tiếp.

b.

Xét tam giác $BFH$ và $CFA$ có:

$\widehat{BFH}=\widehat{CFA}=90^0$

$\widehat{FBH}=\widehat{FBE}=\widehat{FCE}=\widehat{FCA}$ (do $BCEF$ là tgnt)

$\Rightarrow \triangle BFH\sim \triangle CFA$ (g.g)

$\Rightarrow \frac{BF}{CF}=\frac{BH}{CA}$

$\Rightarrow BF.CA=BH.CF$

c.

Kéo dài $AO$ cắt $(O)$ tại $M$ thì $O$ là trung điểm $AM$.

$K$ là trung điểm $BC$ nên $OK\perp BC$,  AH\perp BC$ (do $H$ là trực tâm) 

$\Rightarrow OK\parallel AH$

Có: $\widehat{ABM}=\widehat{ACM}=90^0$ (góc nt chắn nửa đường tròn) 
$\Rightarrow AB\perp BM, AC\perp CM$

Mà $CH\perp AB, BH\perp AC$ nên $BM\parallel CH, CM\parallel BH$

$\Rightarrow BHCM$ là hình bình hành (tứ giác có 2 cặp cạnh đối song song) 
$\Rightarrow HM, BC$ cắt nhau tại trung điểm $K$ của $BC$

$\Rightarrow H,K,M$ thẳng hàng.

Tam giác $AHM$, áp dụng định lý Talet có:

$\frac{OK}{AH}=\frac{OM}{AM}=\frac{1}{2}$

Hình vẽ:

Vì D,E,M thẳng hàng nên ta có: \(\dfrac{DB}{DC}\times\dfrac{EC}{EA}\times\dfrac{MA}{MB}=1\)

=>\(\dfrac{MA}{MB}\times2\times1=1\)

=>\(\dfrac{MA}{MB}=\dfrac{1}{2}\)

=>A là trung điểm của MB

=>AM=AB

Kẻ DK//AC(K\(\in\)BC)

DK//AC

=>\(\widehat{DKB}=\widehat{ACB}\)

mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)

nên \(\widehat{DKB}=\widehat{DBK}\)

=>DK=DB

mà DB=CE

nên DK=CE

Xét ΔMDK và ΔMEC có

\(\widehat{MDK}=\widehat{MEC}\)(DK//CE)

DK=EC

\(\widehat{MKD}=\widehat{MCE}\)(DK//CE)

Do đó: ΔMDK=ΔMEC
=>DM=EM

A B C E D M E

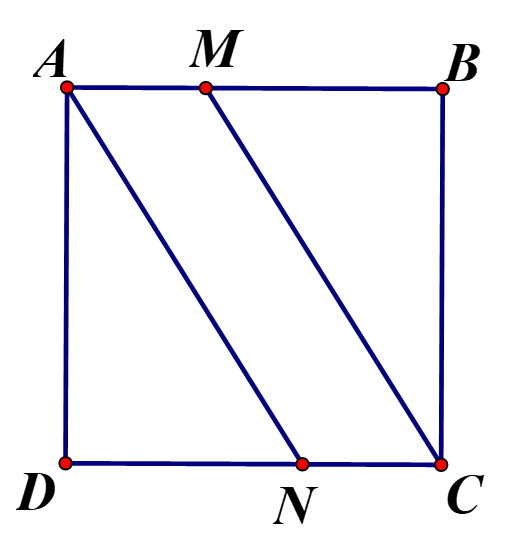
Đặt AM=NC=x��=��=�

Vì {AM//NCAM=NC⇒AMCN��//����=��⇒���� là hình bình hành ⇒SAMNC=60x⇒�����=60�

Vì SAMCN=SABCD⇒60x=6028⇔x=7,5(cm)�����=�����⇒60�=6028⇔�=7,5��

Vậy M  cách A  7,5cm,7,5��,N cách C 7,5cm

a:

b:

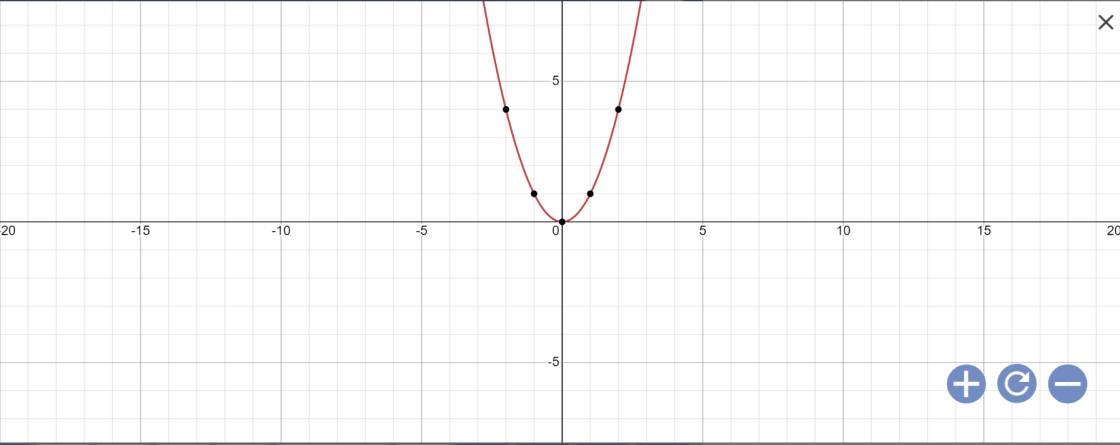
a: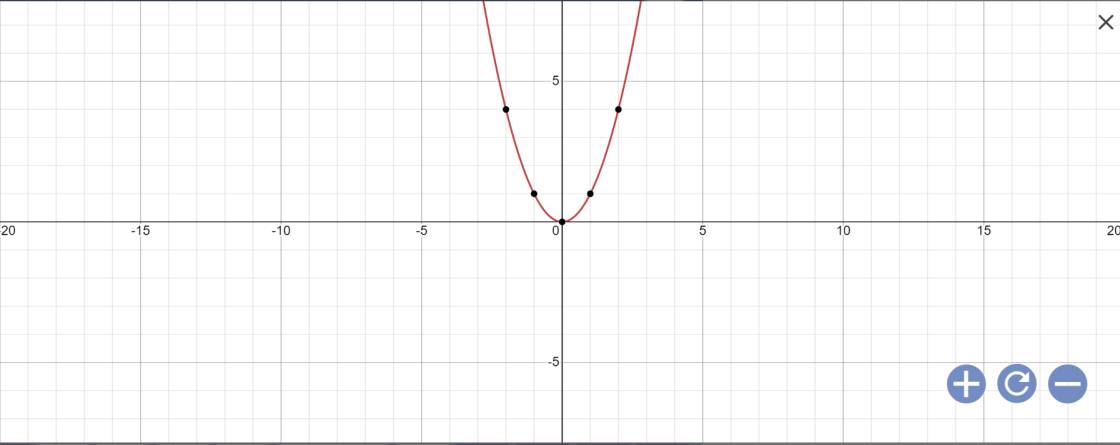 

b: Phương trình hoành độ giao điểm là:

\(x^2=\left(m-2\right)x+6\)

=>\(x^2-\left(m-2\right)x-6=0\)

\(a\cdot c=1\cdot\left(-6\right)=-6< 0\)

=>(P) luôn cắt (d) tại hai điểm phân biệt

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m-2\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)

\(x_2^2-x_1x_2+\left(m-2\right)x_1=16\)

=>\(x_2^2+x_1\left(x_1+x_2\right)-x_1x_2=16\)

=>\(x_2^2+x_1^2=16\)

=>\(\left(x_1+x_2\right)^2-2x_1x_2=16\)

=>\(\left(m-2\right)^2-2\cdot\left(-6\right)=16\)

=>\(\left(m-2\right)^2=4\)

=>\(\left[{}\begin{matrix}m-2=2\\m-2=-2\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}m=4\\m=0\end{matrix}\right.\)

Một hình bình hành có chiều cao là 9cm và bằng 3/4 độ dài đáy. Diện tích hình bình hành đó là 108 cm vuông

Độ dài đáy là 9:3/4=12(cm)

Diện tích hình bình hành là 9x12=108(cm²)

Xét tam giác AEB và tam giác CFD ta có 

AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt) 

Vậy tam giác AEB = tam giác CFD ( c.g.c ) 

=> AE = FC ( 2 cạnh tương ứng ) (1)

tương tự với tam giác AFD = tam giác EBC 

=> AF = EC (2) 

Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF 

Xét tam giác AEB và tam giác CFD ta có 

AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt) 

Vậy tam giác AEB = tam giác CFD ( c.g.c ) 

=> AE = FC ( 2 cạnh tương ứng ) (1)

tương tự với tam giác AFD = tam giác EBC 

=> AF = EC (2) 

Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF